Capítulo 4 Amostragem Aleatória Simples

A amostragem aleatória simples é um plano básico de amostragem que tanto pode ser utilizado diretamente na seleção de uma amostra como ser parte de outros planos amostrais como, por exemplo, Amostragem Estratificada, que serão tratados mais adiante.

4.1 Planos amostrais e algoritmos de seleção

O planejamento da amostra de uma pesquisa requer a definição dos seguintes componentes fundamentais:

C1. Que método será usado para seleção da amostra?
C2. Qual será o tamanho da amostra?
C3. Que estimadores serão usados para os parâmetros de interesse?
C4. Como será feita a avaliação da precisão das estimativas, isto é, como será feita a estimação da variância dos estimadores empregados?

Os componentes C1 e C2, em conjunto, dão origem à especificação do plano amostral. Já os componentes C3 e C4 dão origem à especificação dos métodos de estimação da pesquisa.

Para aplicar um plano amostral qualquer $p(s)$ (a função que associa a cada amostra possível $s$ uma probabilidade de esta ser a amostra selecionada) precisamos contar com um algoritmo de seleção. Um algoritmo de seleção é um método que permite selecionar as unidades da amostra $s$ de tal forma que a probabilidade de ser $s \in S$ a amostra selecionada seja igual a $p(s)$.

Há dois tipos principais de algoritmos de seleção: algoritmos baseados em sequências de sorteios, e algoritmos baseados em processamento sequencial de listas ou cadastros. Algoritmos baseados em sequências de sorteios são aplicados mediante realização de uma série de experimentos aleatórios, chamados sorteios ou extrações. Em cada sorteio, uma unidade é selecionada da população inteira ou de um subconjunto especificado da população, resultando em uma unidade selecionada para a amostra. Ao fim da série de sorteios, fica identificada a amostra selecionada para a pesquisa.

Algoritmos baseados em sequências de sorteios podem ser executados de duas formas distintas: os sorteios podem ser feitos de forma independente, o que implica que unidades já selecionadas podem eventualmente ser selecionadas mais vezes (sorteios com reposição), ou podem ser feitos de forma dependente ou condicional aos resultados dos sorteios antecedentes, geralmente para assegurar que unidades já selecionadas não possam ser selecionadas mais de uma vez (sorteios sem reposição).

Os algoritmos de seleção baseados em processamento sequencial de listas são aplicados mediante realização de uma série de experimentos aleatórios, executados sequencialmente para cada unidade do cadastro ou lista. Cada experimento vai resultar na inclusão ou exclusão dessa unidade da amostra $s$. Algumas vezes tais algoritmos podem terminar sem a necessidade de percorrer todo o cadastro ou lista.

Neste capítulo vamos ilustrar estes conceitos com um tipo de plano amostral bem simples. Mas as ideias básicas aqui introduzidas são aplicáveis de maneira geral a muitas outras situações de interesse.

4.2 Amostragem aleatória simples com reposição

A Amostragem Aleatória Simples Com Reposição - AASC é um plano amostral probabilístico básico, implementado por meio de um algoritmo de seleção no qual um número $n$ prédeterminado de sorteios é feito, sendo em cada sorteio selecionada uma unidade da população (de tamanho $N$). Nesse plano, os sorteios são feitos de forma independente uns dos outros, isto é, com reposição das unidades na população antes da aplicação dos sorteios subsequentes. A seleção da amostra é feita de tal forma que todas as unidades da população têm a mesma chance de ser incluídas na amostra em cada sorteio, e essa probabilidade é igual a $1/N$.

A forma usual de selecionar a amostra consiste em realizar $n$ sorteios consecutivos, sendo cada seleção independente das anteriores. No primeiro passo, é selecionada a primeira unidade $i_1$ de $U$ com probabilidade $1/N$. Esse processo é repetido $n-1$ vezes, sempre de forma independente, e são então selecionadas as unidades $i_2,...,i_k,...,i_n$ nos sorteios seguintes para compor a amostra. Cabe notar que as unidades já selecionadas podem ser repetidas na amostra. Em consequência, o número de amostras possíveis é $N^n$.

AASC é raramente usada na prática, pois é ineficiente em comparação com a amostragem sem reposição de igual tamanho inicial $n$, pelo fato de não incorporar nova informação quando a mesma unidade é selecionada mais de uma vez para a amostra. Na AASC o tamanho efetivo da amostra é $m \le n$, onde $m$ designa o número de unidades distintas selecionadas.

Considere os dados amostrais para a variável $y$ sob AASC, representados por $\{y_{i_1}, y_{i_2},\dots, y_{i_k},\dots, y_{i_n}\}$. Tais valores são observações de variáveis aleatórias $Y_1, Y_2, ..., Y_k, ..., Y_n$ independentes e identicamente distribuídas - IID, com distribuição comum dada conforme descrito na Tabela 4.1.

Unidade populacional $(i)$	1	2	$\dots$	$N$	Soma na linha
Valores que $Y_k$ pode assumir $(y_i)$	$y_1$	$y_2$	$\dots$	$y_N$	$Y$
Probabilidades $[P(Y_k = y_i)]$	$1/N$	$1/N$	$\dots$	$1/N$	1

4.2.1 Estimação do total e média populacionais sob AASC

Lembrando o princípio de estimação que está por trás do estimador tipo Horvitz-Thompson, que consiste em multiplicar cada valor observado na amostra por um peso igual ao inverso de sua probabilidade de inclusão, considere a variável aleatória $Z_k = Y_k / (1/N) = N Y_k$. A cada sorteio de uma unidade para a amostra sob AASC, esta variável aleatória fornece um estimador não viciado para o total populacional $Y$:

\[ E(Z_k) = E \left( N Y_k \right) = \displaystyle \sum_{i \in U} (N y_i) \frac{1}{N} = Y \]

É também fácil mostrar que a variância de $Z_k, \, \, \forall \, \, k = 1, 2, ..., n$ é dada por:

\[ V_{AASC} (Z_k) = V_{AASC} \left( N Y_k \right) = \displaystyle \sum_{i \in U} ({N y_i - Y})^2 \frac{1}{N} = N^2 \sigma_y^2 \]

onde $\sigma_y^2 = \displaystyle \frac{1}{N} \sum_{i \in U} ({y_i - \overline{Y}})^2$.

Com estes resultados, e considerando que sob AASC os dados são obtidos mediante a realização de $n$ sorteios independentes e realizados em condições idênticas, tem-se que um estimador não viciado - ENV para $Y$ é dado por:

\[ \widehat{Y}_{AASC} = \displaystyle \frac {1}{n} \sum_{k = 1}^{n} Z_k = \displaystyle \frac {N}{n} \sum_{k = 1}^{n} Y_k = \displaystyle \frac {N}{n} \sum_{k = 1}^{n} y_{i_k} = \displaystyle \frac {N}{n} \sum_{i \in s} y_i = N \overline{y}\,\,\tag{4.1} \]

onde $\overline{y} = \displaystyle \frac {1}{n} \sum_{k = 1}^{n} y_{i_k} = \displaystyle \frac {1}{n} \sum_{i \in s} y_i$ é a média dos valores observados na amostra.

Segue-se também que a variância deste estimador do total é dada por:

\[ V_{AASC} (\widehat{Y}_{AASC}) = \displaystyle N^2 \sigma_y^2 / n\,\,\tag{4.2} \]

A estimação dessa variância pode ser feita sem viés usando o estimador:

\[ \widehat{V}_{AASC} (\widehat{Y}_{AASC}) = \displaystyle N^2 \widehat S_y^2 / n\,\,\tag{4.3} \] onde $\widehat S_y^2 = \displaystyle \frac{1}{n-1} \sum_{i \in s} ({y_i - \overline{y}})^2$ é um ENV para a variância $\sigma_y^2$.

A estimação não viciada da média populacional $\overline{Y}$ pode ser feita dividindo o ENV do total $Y$ por $N$, ou seja, $\widehat Y_{AASC}/N$, o que resulta em usar o estimador média amostral simples $\overline{y}$ como estimador da média populacional.

A variância e estimador de variância correspondentes são também facilmente obtidos, uma vez que ${V}_{AASC} (\overline{y}) = V_{AASC} (\widehat{Y}_{AASC}) / N^2$.

A Tabela 4.2 apresenta um resumo dos estimadores do total, média e respectivas variâncias sob AASC.

Estimador
$\widehat{Y}_{AASC} = \displaystyle \frac {N}{n} \sum_{i \in s} y_i = N \, \overline{y}$
$\overline{y}=\displaystyle\frac{1}{n} \displaystyle \sum_{i \in s} y_i$
$\widehat S^2_y = \displaystyle \frac{1}{n-1} \sum_{i\in s} ({y_i-\overline{y}})^2$
$\widehat V_{AASC}(\widehat{Y}_{AASC}) = N^2 \widehat S_y^2 / n$
$\widehat V_{AASC}(\overline{y}) = \widehat S_y^2 / n$

Para provas destes resultados, ver, por exemplo, o Teorema 3.3 de Bolfarine e Bussab (2005).

Note que o estimador $\widehat{Y}_{AASC}$ para o total não é o estimador tipo Horvitz-Thompson para este plano amostral. Ver o Exercício 4.1 para uma discussão dessa questão.

A importância da AASC é principalmente teórica: através dela se mostra que é possível obter amostras de forma simples, cujos dados são utilizáveis mediante a aplicação de procedimentos convencionais da Inferência Estatística clássica. Por exemplo, a estimação não enviesada da média populacional $\overline{Y}$ pode ser feita simplesmente com o estimador média amostral $\overline{y}$, e a obtenção das propriedades deste estimador fica facilitada porque as variáveis aleatórias correspondentes aos valores das observações na amostra são IID, mesmo quando a população alvo tem tamanho finito. Ainda mais, o estimador $\overline{y}$ da média $\overline{Y}$ continua válido mesmo quando não se propõe um modelo estocástico para descrever a distribuição dos valores da população, sendo este estimador não viciado independente da forma que tem a distribuição dos valores da população. Tudo isso justifica a apresentação da AASC dentro do conjunto de técnicas abordadas neste livro.

Na prática, entretanto, é raro surgirem aplicações deste plano amostral. O motivo principal, como já indicado, é que AASC é ineficiente em comparação com a amostragem aleatória simples sem reposição de igual tamanho, como vamos mostrar na sequência.

4.3 Amostragem aleatória simples sem reposição

A Amostragem Aleatória Simples sem reposição - abreviada por AAS é um plano amostral similar à AASC, sendo que neste caso cada unidade da população pode aparecer na amostra no máximo uma única vez, isto é, não pode haver repetição de unidades na amostra. Na verdade, AAS é qualquer procedimento de seleção que garanta que todas as amostras de tamanho $n$ da população de tamanho $N$ têm a mesma probabilidade de serem escolhidas. Como existem $\binom{N}{n} = \frac{N!}{n!(N-n)!}$ amostras distintas em $S$, então $p(s) = 1/\binom{N}{n},$ $\forall\, s\in S$, onde $s$ é qualquer subconjunto de $n$ inteiros distintos entre os inteiros de 1 a $N$.

Na AAS duas determinações da amostra são consideradas iguais quando constituídas das mesmas unidades da população, não importando a ordem de seleção dessas unidades.

A seleção da amostra pode ser feita realizando-se $n$ sorteios consecutivos, de modo tal que em cada sorteio todas as unidades da população ainda não selecionadas têm igual chance de ser sorteadas, enquanto que as unidades já eventualmente selecionadas não mais participam do sorteio.

A AAS é um procedimento simples e básico da teoria e prática de amostragem, tendo importância não só pelas aplicações diretas como também por servir de base para muitos outros planos amostrais mais complexos. As ideias principais de amostragem podem ser com ele desenvolvidas.

4.3.1 Algoritmo “convencional” para selecionar uma AAS

O algoritmo “convencional” para a seleção na AAS sugerido pelos livros-texto mais conhecidos em amostragem consiste nos seguintes passos:

Selecione a primeira unidade dentre as $N$ unidades de $U$ com probabilidades iguais a $1/N$, resultando na seleção da unidade $i_1$.
Selecione a segunda unidade dentre as $N-1$ unidades ainda não selecionadas de $U$ com probabilidades iguais a $1/(N-1)$, resultando na seleção da unidade $i_2 \ne {i_1}$.
Prossiga com a seleção de uma unidade por sorteio, sempre excluindo de cada novo sorteio as unidades já selecionadas em sorteios anteriores, até a seleção da $n$-ésima unidade dentre as $N-n+1$ unidades de $U$ que permanecem não selecionadas após $n-1$ sorteios, com probabilidades iguais a $1/(N-n+1)$, resultando na seleção da unidade $i_n \ne {...} \ne {i_2} \ne {i_1}$.

Tal algoritmo fornecia a regra para seleção manual com uso de tabelas de números aleatórios antes do aparecimento e uso de computadores para seleção de amostras. A aplicação deste algoritmo em computador é bastante ineficiente, devido à necessidade de percorrer várias vezes uma lista que pode ser bem grande: a das unidades ainda não selecionadas. Para enfrentar esta dificuldade, foram propostos diversos algoritmos mais eficientes na literatura. Apresentaremos aqui apenas dois, ambos baseados em processamento sequencial de listas, que se destacam por sua simplicidade.

4.3.2 Algoritmo de Hàjek para selecionar AAS

Este algoritmo foi proposto por Hàjek (1960) e consiste nos seguintes passos:

Passo 1: Para cada $i\in U$, associe um número pseudoaleatório $a_i$, onde os $a_i$ são determinações de variáveis aleatórias IID $A_1, A_2, ..., A_N$, todas com distribuição $U(0;1)$, conforme apresentado na Tabela 4.3.

Rótulo da unidade $(i)$	1	2	$\dots$	$N$
Número pseudoaleatório $(a_i)$	$a_1$	$a_2$	$\dots$	$a_N$

Passo 2: Ordene a população segundo os números pseudoaleatórios $a_1, a_2, ..., a_N$, obtendo uma permutação aleatória dos rótulos das unidades populacionais, conforme apresentado na Tabela 4.4.

Rótulo permutado da unidade $(i)$	$i_1$	$i_2$	$\dots$	$i_N$
Número pseudoaleatório ordenado $a_{(i)}$	$a_{(1)}$	$a_{(2)}$	$\dots$	$a_{(N)}$

A notação $a_{(i)}$ indica o valor posicionado na $i$-ésima posição na sequência ordenada dos valores dos números pseudoaleatórios, isto é, corresponde à $i$-ésima estatística de ordem da sequência $a_1 , a_2 , \dots , a_N$.

Passo 3: Para selecionar uma amostra de tamanho $n$, inclua na amostra uma sequência de $n$ rótulos consecutivos quaisquer, na ordem em que aparecem nesta permutação.

Por exemplo, os rótulos $\{i_1, i_2, ..., i_n\}$ fornecem uma AAS.

Outro exemplo: os rótulos $\{i_{N-n+1}, i_{N-n+2}, ..., i_N\}$ também fornecem uma AAS de tamanho $n$ de $U$.

O algoritmo de Hàjek requer duas passagens sobre a lista, mais uma operação de ordenação dos números aleatórios. Oferece grande ganho de eficiência em comparação com o algoritmo convencional, mas ainda não é o mais eficiente.

Exemplo 4.1 Suponha uma população de tamanho $N=1000$ unidades da qual se deseja selecionar uma amostra de tamanho $n=20$ unidades, utilizando o algoritmo de Hàjek.

# Algoritmo de Hàjek
N=1000
n=20
# Gerando os índices da população e os correspondentes pseudoaleatórios 
U=data.frame(1:N,runif(N, min = 0, max = 1))
names(U)=c("i","aleat")
# Ordenando segundo os aleatórios gerados (a ordenação pode ser crescente ou decrescente)
s=U[order(U$aleat),]
s=s[1:n,]
rownames(s)=c(1:n)
# A amostra será formada pelas unidades seguintes
s

##      i        aleat
## 1  533 0.0004144621
## 2  764 0.0006138405
## 3  401 0.0007732986
## 4   47 0.0012060753
## 5  917 0.0016601470
## 6  495 0.0018513452
## 7  200 0.0023315565
## 8  650 0.0023530559
## 9  816 0.0032924507
## 10 446 0.0047138187
## 11 909 0.0061093222
## 12 138 0.0077196558
## 13 813 0.0078781522
## 14 772 0.0094342213
## 15 722 0.0096805156
## 16 491 0.0128703555
## 17 513 0.0149302445
## 18 464 0.0165410258
## 19 109 0.0173275156
## 20 605 0.0182817036

4.3.3 Algoritmo de Fan, Muller e Rezucha para selecionar AAS

Este algoritmo foi proposto por Fan et al. (1962) e consiste nos seguintes passos:

Como no algoritmo anterior, sejam $a_i, \, i = 1, 2, ..., m$, determinações de variáveis aleatórias IID $A_1, A_2, ..., A_m$, todas com distribuição $U(0;1)$.

Processe sequencialmente a lista, para as unidades $i = 1, 2, 3, ..., m$, incluindo na amostra as unidades $i$, tais que $a_i < \frac{n - k_{i-1}}{N - i + 1}$, onde $k_{i-1}$ é o número de unidades selecionadas até o processamento da unidade $i-1$. Após processar cada unidade da lista, atualize o número de unidades já incluídas na amostra. Interrompa o processamento quando $k_{m} = n$, o que ocorre quando for processada a unidade de ordem $m$. Note que $m$ é uma quantidade aleatória, que vai variar no intervalo $n \le m \le N$, e corresponde ao número de sorteios necessários para conseguir uma AAS de tamanho $n$ da população de tamanho $N$.

O algoritmo de Fan, Muller e Rezucha, para selecionar uma AAS de tamanho $n$ de uma população de $N$ unidades, pode ser resumido nos seguintes passos:

$i\leftarrow 0$
$i\leftarrow I+1$
Para a unidade $U_i$ gere um número pseudolaeatório $a_i\sim U(0;1)$
Se $a_i<n/N$
- Inclua $U_i$ na amostra
- $N\leftarrow N-1$
- $n\leftarrow n-1$
Se $a_i\ge n/N$
- $N\leftarrow N-1$
Se $n=0$ ou $N=0$ pare
Retorne ao passo 2

Este algoritmo é muito eficiente em comparação com os anteriores, porque requer processar a lista no máximo uma vez, e pode nem mesmo requerer chegar ao fim da lista: a amostra pode ser selecionada por completo bem antes de chegar ao final da lista. Apesar de sua simplicidade e eficiência, há alternativas ainda mais eficientes, que entretanto não serão discutidas aqui. Caso o leitor necessite implementar um algoritmo para seleção de uma AAS, recomendamos o emprego deste algoritmo. Será suficientemente bom para a maioria das aplicações práticas.

Exemplo 4.2 Vamos repetir o Exemplo 4.1, utilizando algoritmo de Fan, Muller e Rezucha.

# Algoritmo de Fan, Muller e Rezucha para seleção de uma amostra 
# de n unidades de uma população de tamanho N
N = 1000
n = 20
s = NULL # Vetor para guardar os índices das unidades da amostra
i = 0 # Contador das unidades populacionais
j = 0 # Contador das unidades da amostra
while (n > 0 & N > 0) {
  i=i+1 
# Geração de número pseudoaleatório uniforme entre 0 e 1 e
# comparação com a fração amostral atualizada. Se for menor
# a unidade entra na amostra.
  if (runif(1) < n/N){
    j = j+1
    s[j]=i
    n = n-1 # Atualiza quantas unidades faltam para a amostra
  }
  N = N-1 # Atualiza unidades da população sujeitas à seleção
}
s=data.frame(s)
names(s)=c("i")
# A amostra será formada pelas unidades seguintes
s

##      i
## 1   86
## 2  138
## 3  164
## 4  224
## 5  227
## 6  361
## 7  413
## 8  614
## 9  688
## 10 796
## 11 811
## 12 819
## 13 845
## 14 852
## 15 908
## 16 929
## 17 946
## 18 988
## 19 994
## 20 998

4.3.4 Probabilidades de inclusão sob AAS

Como já indicado no Capítulo 3, tratar com as distribuições de aleatorização $p(s)$ sob AAS pode ser complicado do ponto de vista prático. Särndal et al. (1992), página 29, mencionam que numa população com $N = 1.000$ unidades, o conjunto $S$ de amostras AAS possíveis de tamanho $n=40$ tem dimensão $\binom{N}{n} = \binom{1.000}{40} = 5,6 \times 10^{71}$. Se a população tivesse $N = 5.000$ e a amostra tamanho $n = 200$, a dimensão de $S$ cresceria para $\binom{5.000}{200} = 1,4 \times 10^{363}$. Portanto, a enumeração de todas as amostras possíveis seria tarefa complicada, mesmo com computadores poderosos.

Note que os tamanhos de população e amostra acima são modestos do ponto de vista de aplicações práticas. Foi para eliminar essa dificuldade que introduzimos resumos simples derivados da distribuição $p(s)$. Tais resumos serão suficientes para a obtenção de propriedades de estimadores tais como valor esperado e variância, na maioria das situações de interesse prático. Esses resumos são as probabilidades de inclusão de unidades ou de pares de unidades na amostra.

Tem-se então que:

Sob AAS, $\pi_i = n / N > 0$, $\forall \,i \in U$, desde que $n > 0$.
$f = n / N$ é chamada de fração amostral ou taxa de amostragem.
Estimação de variância sem vício requer $\pi_{ij} > 0$, $\forall\, i,j \in U$. Sob AAS, $\pi_{ij} = \displaystyle \frac{n(n-1)}{N(N-1)} > 0, \,\,\, \forall\, i \ne j \in U$.
Sob AAS, as probabilidades de inclusão $\pi_i$ e $\pi_{ij}$ não dependem de $i$ ou $j$, e essa é a razão da simplicidade desse plano amostral.

Sob AAS de tamanho $n$ de população com $N$, para a variável $\delta_i$ indicadora do evento ‘inclusão da unidade $i$ na amostra $s$’, tem-se:

$E_{AAS} [{\delta_i}] = \displaystyle\frac{n}{N}$

$V_{AAS} [{\delta_i}] = \displaystyle\frac{n}{N} \left(1-\frac{n}{N}\right)$

$COV_{AAS} [{\delta_i},{\delta_j} ] = \displaystyle\frac{n(n-1)}{N(N-1)} - \left(\frac{n}{N}\right)^2 = \frac{n}{N}\left(1-\frac{n}{N}\right)\left(-\frac{1}{N-1}\right)$

Assim, sob AAS a correlação entre duas variáveis indicadoras de inclusão de unidades distintas na amostra é dada por:

$CORR_{AAS} [{\, \delta_i} \, , {\delta_j} ] = -1/(N-1)$, se $i \ne j$

4.3.5 Estimador não viciado do total e média populacionais sob AAS

Usando o estimador não viciado de total tipo Horvitz-Thompson, e substituindo os valores das probabilidades de inclusão de primeira ordem, obtém-se:

\[ \widehat Y_{HT} = \displaystyle \sum_{i \in s} \frac{y_i}{\pi_i} = \displaystyle \sum_{i \in s} \frac{y_i}{n/N} = \frac{N}{n} \displaystyle \sum_{i \in s} y_i = N \overline {y} = \widehat{Y}_{AAS}\,\,\tag{4.4} \]

Este é um ENV do total populacional $Y$ e em consequência, $\overline y=\displaystyle\frac{1}{n} \displaystyle \sum_{i \in s} y_i$ é ENV da média populacional $\overline Y$ sob AAS.

A variância do estimador do total sob AAS é dada por:

\[ V_{AAS}(\widehat{Y}_{AAS}) = N^2 \left( 1 - \frac{n}{N} \right) \frac{S^2_y}{n} = N^2 \left( \frac{1}{n} - \frac{1}{N} \right) S^2_y\,\, \tag{4.5} \] então, a variância do estimador da média sob AAS é dada por:

\[ V_{AAS} (\overline{y}) = \displaystyle \left( \frac{1}{n} - \frac{1}{N} \right) S^2_y\,\, \tag{4.6} \]

Um ENV da variância do estimador de total é dado por:

\[ \widehat V_{AAS} (\widehat{Y}_{AAS}) = \displaystyle N^2 \left( 1 - \frac{n}{N} \right) \frac{\widehat S^2_y}{n} = N^2 \left( \frac{1}{n} - \frac{1}{N} \right) \widehat S^2_y \,\, \tag{4.7} \]

onde $\widehat S^2_y = \displaystyle \frac{1}{n-1} \sum_{i \in s} ({y_i - \overline{y}})^2$, como já definido.

Logo, um ENV da variância do estimador da média sob AAS é dado por:

\[ \widehat V_{AAS} (\overline{y}) = \displaystyle \left( \frac{1}{n} - \frac{1}{N} \right) \widehat S^2_y\,\, \tag{4.8} \]

A Tabela 4.5 apresenta um resumo dos estimadores do total, média e respectivas variâncias sob AAS.

Estimador
$\widehat{Y}_{AAS} = \displaystyle \frac {N}{n} \sum_{i \in s} y_i= N \overline{y}$
$\overline{y} = \displaystyle\frac{1}{n} \displaystyle \sum_{i \in s} y_i$
$\widehat S^2_y = \displaystyle \frac{1}{n-1} \sum_{i \in s} \left( {y_i - \overline{y}} \right)^2$
$\widehat V_{AAS}(\widehat{Y}_{AAS}) = \displaystyle N^2 \left( \frac{1}{n} - \frac{1}{N} \right) \widehat S^2_y$
$\widehat {V}_{AAS} (\overline{y}) = \displaystyle \left( \frac{1}{n} - \frac{1}{N} \right) \widehat S^2_y$

Notas:

O termo $(1 - n/N) = (1 - f)$ é chamado de fator de correção para população finita. Quando $n/N \rightarrow 1$, o tamanho da amostra se aproximando do tamanho da população, então $(1 - n/N) \rightarrow 0$ . Ou seja: com amostras grandes as variâncias das estimativas tendem a ser pequenas.
Se a fração amostral $f = n/N$ for pequena (da ordem de 1% ou 2%), então a correção de população finita pode ser ignorada, pois $(1 – f) \doteq 1$. Quando $f \doteq 0$, a AAS (amostragem sem reposição) e AASC (com reposição) tem comportamento semelhante em relação à precisão das estimativas. Intuitivamente, isso ocorre porque no caso em que a amostra é muito pequena em relação ao tamanho da população a probabilidade de uma unidade da população ser selecionada mais de uma vez é pequena.

4.3.6 Distribuição da média amostral

Sob repetições do procedimento de seleção segundo AAS, $\overline{y}$ tem uma distribuição de probabilidades. A distribuição exata de $\overline{y}$ depende da distribuição de $y$ na população, do tamanho da amostra $n$ e do plano amostral $p(s)$, que neste caso, é AAS. Isto resulta numa situação complicada, que pode ser resolvida considerando a Distribuição Assintótica da Média Amostral.

Se $n$ for grande e $f = n/N$ for pequena, o Teorema Central do Limite - ver Hàjek (1960) - pode ser usado para obter a distribuição aproximada:

\[ \frac{\overline {y}-E_{AAS}(\overline{y})}{\sqrt{V_{AAS}(\overline{y})}}=\frac{\overline {y}-\overline{Y}}{\displaystyle\sqrt{\left(\frac{1}{n}-\frac{1}{N}\right)S^2_y}}\approx N(0;1)\,\,\tag{4.9} \]

onde $N(0;1)$ denota uma variável aleatória com distribuição normal padrão com média zero e variância um. Mais detalhes podem ser obtidos em Cochran (1977), Seções 2.8 e 2.15, ou em Särndal et al. (1992), Seção 2.11.

É com base nessa distribuição assintótica que se pode fazer inferência por intervalos de confiança para a média populacional, e com base nesta ideia, medir a margem de erro de uma estimativa da média populacional. Um intervalo de confiança de nível $(1 - \alpha)%$ para a média populacional sob AAS é dado por:

\[ IC_{AAS} (\overline{Y} ; 1 - \alpha) = \left [ \overline {y} \mp z_{\alpha/2} \sqrt{\widehat {V}_{AAS}(\overline{y})} \right ]\,\,\tag{4.10} \]

onde $z_{\alpha/2}$ é a abscissa da distribuição $N(0;1)$ que deixa à sua direita área igual a ${\alpha/2}$.

A semiamplitude do intervalo de confiança para o parâmetro nos fornece uma ideia da margem de erro que se tem ao estimar o parâmetro. A margem de erro da estimativa de média é, então, estimada por:

\[ \widehat{ME}_{AAS} (\overline{y}) = z_{\alpha/2} \sqrt{\widehat {V}_{AAS}(\overline{y})}\,\,\tag{4.11} \] Note que a margem de erro é também uma quantidade que se pode estimar a partir da amostra selecionada e observada. Essa é uma das vantagens importantes da amostragem probabilística, pois nos fornece além das estimativas pontuais diretas dos parâmetros de interesse, também indicativos da incerteza associada a tais estimativas.

4.3.7 Comparação dos planos de amostragem aleatória simples com e sem reposição

Do ponto de vista prático, a principal diferença entre os planos amostrais AASC e AAS é que, no primeiro, unidades populacionais podem ser selecionadas mais de uma vez para compor a amostra, o que não é possível no segundo. Ambos os planos permitem usar estimadores não viciados bem simples para o total e a média populacionais, mas o plano AAS fornece estimadores com menor variância para iguais tamanhos de amostra, sendo por isso mesmo preferido na prática.

Em resumo, as diferenças da amostragem aleatória simples sem reposição - AAS para a com reposição - AASC estão nos seguintes aspectos:

AAS evita repetição de seleção de unidades para a amostra.
AAS leva a um modelo estatístico diferente: as observações amostrais não são independentes.
AAS diminui o conjunto $S$ de amostras possíveis.
AAS mantém a simplicidade dos estimadores.
AAS permite estimação mais eficiente da média ou total populacionais sob amostras de igual tamanho.

4.4 Determinação do tamanho da amostra

Nesta seção, procura-se responder à pergunta de que tamanho deve ter a amostra de uma pesquisa. A resposta a essa pergunta depende da resposta a uma de duas perguntas alternativas:

Quanto se pretende gastar na pesquisa?
Qual a precisão desejada (esperada) dos resultados?

A primeira decisão é qual dos dois caminhos seguir para determinar o tamanho da amostra: fixar custo ou precisão?

4.4.1 Tamanho amostral para custo fixado

Se a escolha for determinar o tamanho da amostra fixando parâmetros de custo, recomendamos usar como tamanho de amostra o maior tamanho permitido pelo orçamento (ou tempo) disponível. Nesse caso, não há uma teoria geral pronta para ser aplicada a toda e qualquer pesquisa. Há que estudar a função de custo de cada pesquisa e com base nela, definir o tamanho da amostra.

Exemplo 4.3 Determinando o tamanho de amostra para uma pesquisa junto a empresas

Considere um cenário em que o interesse é realizar uma pesquisa junto a empresas, para estimar alguns totais ou médias. O cliente que demanda a pesquisa informa que tem disponível um orçamento limitado, e que para a atividade de coleta da pesquisa o valor disponível é de R$ 400.000,00 (quatrocentos mil reais).

Após realizar reuniões com o cliente e ter informação mais precisa sobre o questionário e características da pesquisa, o responsável por planejar a amostra estima que coletar dados de cada empresa selecionada para a amostra terá um custo médio de R$ 200 por questionário. Vale também comentar que é importante que, ao estimar o custo médio de coleta por questionário, o planejador da pesquisa deixe margem de segurança para cobrir eventuais dificuldades imprevistas de coleta.

Considerando o orçamento disponível para a coleta, o recomendável seria então usar uma amostra de $n = 400.000 / 200 = 2.000$ empresas.

Após calcular este tamanho de amostra, o responsável pelo planejamento da amostra deve comunicar ao cliente alguma ideia de que precisão seria possível alcançar com esse tamanho de amostra e orçamento, ao menos para os principais parâmetros de interesse da pesquisa. Isto ajudaria a evitar frustrações ou reclamações após a coleta dos dados e a obtenção das estimativas de interesse.

4.4.2 Tamanho amostral para precisão fixada

Se a escolha for determinar o tamanho amostral para garantir resultados com certa precisão (margem de erro) especificada, devemos também especificar o grau de confiança a adotar.

Exemplos:

“Desejamos estar 90% confiantes de que a estimativa da média está a no máximo $\pm 10$ unidades do valor verdadeiro.”
“Desejamos que a estimativa da média não se afaste do valor verdadeiro mais que 10%, com probabilidade 0,95.”

No item 1 acima, estabelecemos a margem de erro - $D$ igual à semiamplitude do intervalo de confiança para $\overline Y$ em unidades da variável resposta, para um determinado nível de confiança (90% ou 0,90).

No item 2 acima, estabelecemos a margem de erro relativo - $D_r$ a semiamplitude do intervalo de confiança para $\overline Y$ em termos relativos, aceitando um erro relativo máximo de 10% do valor de $\overline Y$, para um determinado nível de confiança (95% ou 0,95).

Para determinar o tamanho amostral para precisão fixada, a ideia é usar a informação disponível sobre a distribuição do estimador e alguma informação prévia existente sobre a população.

Sabe-se que para $n$ grande e $f = n/N$ limitada longe de 1:

\[\frac {\overline {y} - \overline{Y}} {\displaystyle \sqrt{\left(\frac{1}{n}-\frac{1}{N}\right)S_y^2}} \approx N(0;1)\] Segue-se então que:

\[P \left(\frac{|\overline {y}-\overline{Y}|}{\displaystyle\sqrt{\left(\frac{1}{n}-\frac{1}{N}\right)S_y^2}}\le z_{\alpha/2}\right)= 1-\alpha\]

onde $z_{\alpha/2}$ é o valor da abscissa da distribuição Normal padrão tal que $P[N(0;1) > z_{\alpha/2}] = \alpha /2$.

Segue-se então que:

\[P \left(|\overline {y}-\overline{Y}|\le z_{\alpha/2}{\sqrt{\left(\frac{1}{n}-\frac{1}{N}\right)S_y^2}}\right)= 1-\alpha\] .

Logo, o erro de estimar $\overline Y$ usando $\overline y$ sob AAS é menor ou igual a $z_{\alpha/2} {\sqrt {\left( \frac{1}{n} - \frac{1}{N} \right) S_y^2}}$ com probabilidade $1-\alpha$.

Então se desejamos estimar $\overline Y$ com um erro máximo de $\pm 10$ unidades, com um nível de confiança de 90% (o que significa que o valor tabelado $z_{\alpha/2}= 1,645$), basta fazer:

\[z_{\alpha/2} {\sqrt{ \left( \frac{1}{n} - \frac{1}{N} \right )S_y^2}} = 1,645 \sqrt{ \left( \frac{1}{n} - \frac{1}{N} \right) S_y^2} = 10\]

e resolver a equação em relação ao tamanho amostral $n$.

Logo:

\[1,645 \sqrt{ \left( \frac{1}{n} - \frac{1}{N} \right) S_y^2} = 10 \Rightarrow \left( \frac{1}{n} - \frac{1}{N} \right) S_y^2 = \left( \frac{10}{1,645} \right)^2\]

Segue-se então que:

\[\frac{1}{n} = \left( \frac{10}{1,645} \right)^2 \frac{1}{S_y^2} + \frac{1}{N} \Rightarrow n = \frac{1}{\displaystyle\left( \frac{10}{1,645} \right)^2 \frac{1}{S_y^2} + \frac{1}{N}}\]

Para calcular o tamanho desejado da amostra precisamos conhecer $N$ e $S_y^2$. Seguem algumas sugestões de como fazer para resolver a questão de que $S_y^2$ é também desconhecido:

Usar informações de pesquisas anteriores.
Fazer amostra prévia (amostra piloto) e estimar $S^2_y$ usando $\widehat S_y^2$ com os dados dessa amostra prévia.
Em casos especiais (proporções e outros), usar cota superior para o valor de $S_y^2$.

O caso geral

Seja $D$ a precisão desejada, a margem de erro máximo admissível na estimação de $\overline Y$, a semiamplitude desejada para o intervalo de confiança de $\overline Y$. Seja $1-\alpha$ o coeficiente de confiança desejado para o procedimento. Para intervalos de confiança de 95% usamos $z_{\alpha/2} = 1,96$.

Um intervalo de confiança não é uma especificação sobre uma particular amostra, mas sobre o desempenho do procedimento sob todas as possíveis amostras. Quando se usa um intervalo de confiança de 95% para um parâmetro, isto quer dizer que os intervalos construídos com cerca de 95 de cada 100 amostras selecionadas (sob idênticas condições) cobririam o “verdadeiro” valor do parâmetro de interesse. Para uma amostra específica, selecionada pelo método escolhido, acredita-se que é de 95% a chance que o “verdadeiro” valor seja coberto pelo intervalo: \[[\text{Estimativa} - 1,96 \times \text{desvio padrão; Estimativa} + 1,96 \times \text{desvio padrão}]\]

Assim:

\[\left( \frac{1}{n} - \frac{1}{N} \right) S_y^2 = \left( \frac{D}{z_{\alpha/2}} \right)^2\]

Portanto, o tamanho de uma AAS que assegura precisão $D$ com nível de confiança $1 - \alpha$ é:

\[ n = \displaystyle\frac{1}{\displaystyle\left( \frac{D}{z_{\alpha/2}} \right)^2 \displaystyle\frac{1}{S_y^2} + \frac{1}{N}} = \displaystyle\frac{N z_{\alpha/2}^2 S_y^2} {N{D}^2 + {z_{\alpha/2}^2} S_y^2}\,\,\tag{4.12} \]

Comentários:

A Expressão (4.12) só se aplica para o caso do estimador média amostral $\overline y$ para a média populacional $\overline Y$ sob AAS.
É possível derivar expressões similares para o caso da estimação de totais, e também de outros parâmetros.
Para planos amostrais mais complexos, é mais difícil resolver equações do tipo acima para determinar tamanhos amostrais, e sua alocação em estratos e conglomerados. Entretanto, a ideia de Efeito do Plano Amostral - EPA vai ser útil neste contexto. Ver discussão no Capítulo 12.

Exemplo 4.4 Considere a população formada pelos municípios brasileiros, conforme consta do arquivo ‘MunicBR_dat.rds’. Tendo esta população em mente, imagine que seria usada para seleção de uma amostra AAS de $n=200$ municípios. Imagine que tal amostra seria usada para estimar a média populacional da variável área dos municípios.

Com esta perspectiva, use os dados populacionais para:
1. Calcular a média populacional.
2. Calcular a variância, desvio padrão e coeficiente de variação do estimador usual.
3. Avaliar a margem de erro relativo que a estimativa teria ao nível 95% de confiança.
4. Determinar o tamanho da amostra que seria necessária para estimar a média da área com um erro máximo de 150 km² ao nível de confiança de 95%.
Selecione uma AAS de tamanho $n=200$ e use os dados amostrais para calcular:
1. Uma estimativa da média populacional.
2. Estimativas da variância, desvio padrão e coeficiente de variação da média estimada.
3. Estime a margem de erro relativo que a estimativa obtida no item a teria ao nível 95% de confiança.
4. O tamanho da amostra que seria necessária para estimar a média da área com um erro máximo de 150 km² ao nível de confiança de 95%.
Compare estimativas obtidas no item 2 com os valores obtidos no item 1 e analise/comente.

Solução do Exemplo 4.4 usando R

# Limpa área de trabalho
rm(list = ls())

# Carrega biblioteca(s) requerida(s)
library(sampling)

# Leitura dos dados
MunicBR_dat <- readRDS(file="Dados/MunicBR_dat.rds")
str(MunicBR_dat)

## Classes 'tbl_df', 'tbl' and 'data.frame':    5570 obs. of  6 variables:
##  $ CodMunic : chr  "1100015" "1100023" "1100031" "1100049" ...
##  $ SiglaUF  : chr  "RO" "RO" "RO" "RO" ...
##  $ CodUF    : chr  "11" "11" "11" "11" ...
##  $ Pop      : num  25728 101269 6495 85863 18041 ...
##  $ Area     : num  7067 4427 1314 3793 2783 ...
##  $ Densidade: num  3.64 22.88 4.94 22.64 6.48 ...

# Item 1
# Tamanho da população
(N = nrow(MunicBR_dat))

## [1] 5570

# Tamanho inicial da amostra
(n <- 200)

## [1] 200

# Soluções para item 1
# a. Média populacional
(med_pop <- mean(MunicBR_dat$Area))

## [1] 1526.536

# b. Dispersão do estimador de média sob AAS
(VAR_med_amo <- ((1/n) - (1/N)) * var(MunicBR_dat$Area))

## [1] 151683.3

(DP_med_amo <- sqrt(VAR_med_amo))

## [1] 389.4654

(CV_med_amo <- 100 * DP_med_amo / med_pop)

## [1] 25.51302

# c. Margem de erro relativo do estimador de média sob AAS
(ME_med_amo <- qnorm(0.975)*CV_med_amo)

## [1] 50.00461

# d. Tamanho de amostra para obter margem de erro de 150 ao nível 95%
(D <- 150)

## [1] 150

(n_amo <- (N * qnorm(0.975)^2 * var(MunicBR_dat$Area)) /
          (N * D^2 + qnorm(0.975)^2 * var(MunicBR_dat$Area)))

## [1] 2734.689

(n_amo <- ceiling(n_amo))

## [1] 2735

# Soluções para item 2
# Seleciona amostra
munic_amo <- getdata(MunicBR_dat, srswor(n, N))

# a. Média amostral
(med_amo <- mean(munic_amo$Area))

## [1] 1196.733

# b. Estimativas da dispersão do estimador de média sob AAS
(var_med_amo <- ((1/n) - (1/N)) * var(munic_amo$Area))

## [1] 34192.79

(dp_med_amo <- sqrt(var_med_amo))

## [1] 184.9129

(cv_med_amo <- 100 * dp_med_amo / med_amo)

## [1] 15.45148

# c. Margem de erro relativo do estimador de média sob AAS
(me_med_amo <- qnorm(0.975)*cv_med_amo)

## [1] 30.28435

# d. Tamanho de amostra para obter margem de erro de 150 ao nível 95%
(D <- 150)

## [1] 150

(n_amo_est <- (N * qnorm(0.975)^2 * var(munic_amo$Area)) /
              (N * D^2 + qnorm(0.975)^2 * var(munic_amo$Area)))

## [1] 994.759

(n_amo_est <- ceiling(n_amo_est))

## [1] 995

4.5 Exercícios

Exercício 4.1 Mostre que o estimador $\widehat{Y}_{AASC}$ para o total não é um estimador tipo Horvitz-Thompson.

Exercício 4.2 Considere a população de 338 fazendas produtoras de cana-de-açúcar fornecida no arquivo ‘fazendas_dat.rds’. Esse arquivo contém os dados de algumas variáveis econômicas medidas para cada uma das fazendas dessa população, tais como área plantada com cana-de-açúcar (Area), quantidade colhida de cana (Quant), receita (Receita) e despesa com a produção de cana (Despesa), e algumas variáveis de contexto sobre as fazendas, tais como região de localização (Regiao) e classe de tamanho da fazenda (Classe).

Imagine que há interesse em pesquisar por amostragem essa população de fazendas, visando estimar medidas descritivas da população, tais como os totais das variáveis Quant, Receita e Despesa. O objetivo do exercício é usar os dados fornecidos para estudar o comportamento esperado de um plano amostral. Considere a ideia de selecionar uma amostra de $n=50$ fazendas da população usando AAS.

Use os valores populacionais das variáveis de interesse (Area, Quant e Receita) para calcular os totais populacionais de interesse. Calcule também o desvio padrão - DP e o coeficiente de variação - CV esperados para os estimadores dos totais populacionais de interesse, supondo que o estimador Horvitz-Thompson para o total seria empregado. Compare os resultados para as diversas variáveis.
Selecione efetivamente uma amostra segundo o esquema amostral indicado e use essa amostra para estimar os totais populacionais de interesse, bem como os respectivos DPs e CVs. Compare os resultados com os valores obtidos no item a e comente aspectos dignos de nota.
Use a amostra selecionada por AAS para estimar a variância populacional de Quant e Receita. Use estas informações para dimensionar a amostra necessária para estimar o total com CV de 10% para cada uma das duas variáveis. Ao final, que tamanho de amostra você usaria na pesquisa para atingir o objetivo estabelecido?
Repita 500 vezes o item b, e analise a distribuição resultante das estimativas de total para as variáveis Quant e Receita. Analise, comente.

Exercício 4.3 Para uma população com $N=4$ unidades, cujos valores de uma dada variável de interesse, $y$, são $\{0,\;1,\;2,\;3,\;4\}$:

Liste todas as possíveis AAS de tamanho $n=2$.
Calcule $S^2_y$ e $V_{AAS}(\overline y)$.
Mostre numericamente que $V_{AAS}(\overline y)=\frac {N-n}N \frac {S^2_y}n$.
Mostre numericamente que $E_{AAS}(\widehat S^2_y)=S^2_y$.
Liste todas as possíveis AASC de tamanho $n=2$.
Mostre numericamente que $V_{AASC}(\overline y)= \frac {\sigma^2_y}n$.
Mostre numericamente que $E_{AASC}(\widehat S^2_y)=\sigma^2_y$.

Exercício 4.4 A administração de um parque florestal deseja estimar a população de coelhos e veados no parque nos meses de inverno. Para isso a área da floresta foi dividida, através de um levantamento aerofotométrico, em 10.000 pequenas áreas de aproximadamente 10 m². Uma AAS de $n = 500$ dessas pequenas áreas foi selecionada e foram observados os números de coelhos e veados em cada uma delas, resultando na Tabela 4.6:

Estatísticas	Veados	Coelhos
Média amostral	2,30	4,52
Variância amostral	0,65	0,97

Estime o total de veados do parque e o coeficiente de variação da estimativa.
Estime o total de coelhos do parque e o coeficiente de variação da estimativa.
Observando os CVs estimados, compare e comente sobre a precisão das estimativas de total de veados e coelhos.

Exercício 4.5 Uma grande empresa de construção tem 120 obras em andamento em diversos estágios. Para estimar o total de dinheiro já investido no conjunto das obras, para um relatório gerencial, foram selecionadas 12 delas, por AAS, e verificados os gastos, em Reais, acumulados até aquele momento. Os resultados estão na Tabela 4.7:

Obra	Gasto (Reais)	Obra	Gasto (Reais)
1	35.500	7	26.400
2	36.400	8	32.200
3	32.600	9	28.900
4	38.200	10	34.100
5	30.200	11	38.000
6	29.800	12	27.500

Estime o gasto médio acumulado por obra e a precisão da estimativa, calculando a estimativa do CV.
Estime o gasto total acumulado para as 120 obras e a precisão da estimativa, calculando a estimativa do CV.
Compare as estimativas de precisão obtidas nos itens a e b.

Exercício 4.6 Considere os dados, apresentados na Tabela 4.8, de salários (em 1.000 Reais) pagos no ano de 1997 pelas 5 (cinco) empresas de uma amostra que foi pesquisada de uma população com 250 empresas, onde o plano amostral foi amostragem aleatória simples sem reposição.

Empresa	1	2	3	4	5
Salários pagos (1.000 Reais)	12	100	120	48	60

Estime o total de salários pagos pelas empresas da população, seu respectivo CV e obtenha um intervalo de confiança de 95% para o total populacional de interesse.
Usando a amostra observada como amostra piloto, calcule o tamanho de amostra necessário para estimar o total dos salários com precisão relativa $D_r = 0,10$, ao nível de confiança de 95%.

Exercício 4.7 A Tabela 4.9 mostra os dados amostrais de uma pesquisa feita por uma AAS numa população de 500 unidades.

Frequência $(f_i)$	$y_i$
4	10
3	11
5	12
2	13
4	15
3	17
4	18

Estime a média populacional e construa um intervalo de 95% de confiança para a média.
Usando a amostra apresentada como amostra piloto, calcule um tamanho de amostra suficiente para estimar a média da população de maneira que, com 95% de probabilidade, a margem de erro não ultrapasse a 5% do valor da média.

Exercício 4.8 Foi selecionada uma AAS de 30 unidades de uma população composta por 100 unidades. Uma variável de interesse $y$ foi observada e os valores obtidos foram: 8, 5, 2, 6, 6, 3, 8, 6, 10, 7, 15, 9, 15, 3, 5, 6, 7, 10, 14, 3, 4, 17, 10, 6, 14, 12, 7, 8, 12, 9.

Qual o peso amostral de cada unidade da amostra?
Usando o peso amostral, estime o total populacional de $y$.
Construa um intervalo de 95% de confiança para o total populacional.

Exercício 4.9 Seja a população formada pelos 450 municípios da Região Norte que aparecem no arquivo ‘MunicBR_dat.rds’.

Calcule os seguintes parâmetros populacionais da variável de interesse população (Pop): média populacional e variância populacional.

Supondo desconhecidos os valores da população dos municípios, selecione uma AAS de tamanho $n=40$ e estime os seguintes parâmetros populacionais:

Estime a média populacional.
Estime a variância populacional e a variância do estimador da média populacional.
Construa $IC_{95\%}$ para a média populacional.
Compare, e comente, os resultados estimados na amostra com os valores verdadeiros da população.
A média populacional pertence ao intervalo de confiança construído? O que isso significa?

Exercício 4.10 Um biólogo deseja estimar o total populacional de determinado animal numa reserva florestal. Para isso ele dividiu a floresta em lotes de tamanhos aproximadamente iguais e selecionou uma amostra desses lotes, contando os animais encontrados. A Figura 4.1 mostra, esquematicamente, o mapa da reserva com a divisão feita. A amostra é formada pelos lotes onde aparecem os números de animais encontrados, que foram selecionados usando um processo de AAS.

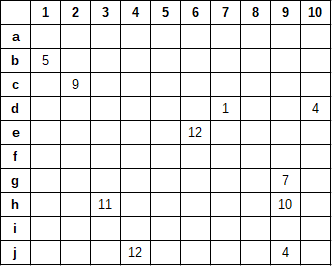
Figura 4.1: Mapa esquemático da reserva com o número de animais encontrados nos lotes selecionados

Faça uma tabela com os dados amostrais.
Use a amostra para estimar o número de animais da espécie em estudo na reserva.
Estime a variância da estimativa do número de animais.
Qual a probabilidade de inclusão, numa amostra de tamanho 10, do lote do canto superior esquerdo do mapa (lote a1)?
Qual o número total de amostras de tamanho 10 possíveis?
Qual a probabilidade de selecionar a amostra do item a?

Unidade populacional \((i)\)	1	2	\(\dots\)	\(N\)	Soma na linha
Valores que \(Y_k\) pode assumir \((y_i)\)	\(y_1\)	\(y_2\)	\(\dots\)	\(y_N\)	\(Y\)
Probabilidades \([P(Y_k = y_i)]\)	\(1/N\)	\(1/N\)	\(\dots\)	\(1/N\)	1

Frequência \((f_i)\)	\(y_i\)
4	10
3	11
5	12
2	13
4	15
3	17
4	18