Capítulo 5 Estimação de Proporções
5.1 Parâmetros populacionais
Um caso especial de parâmetro de interesse para muitos estudos ou pesquisas ocorre quando a variável \(y\) indica se uma determinada unidade populacional tem ou não uma determinada característica ou atributo, ou pertence a um determinado grupo especificado de unidades da população. São exemplos desse tipo as investigações sobre:
- Migrantes entre os habitantes de determinada região.
- Estabelecimentos agropecuários que se dedicam exclusivamente à produção leiteira numa determinada localidade.
- Estudantes do sexo feminino em escolas.
- Sondagens eleitorais, para conhecer qual parcela dos eleitores pretende votar em determinado candidato.
Sendo uma variável indicadora, a variável \(y\) assume, para cada unidade da população, um de dois valores possíveis: o valor \(1\), se a unidade possui o atributo de interesse, ou o valor \(0\), caso a unidade não possua o atributo. Para fins de apresentação, seja \(A \subset U\) o subconjunto das unidades da população \(U\) que possuem o atributo de interesse. Então, para cada unidade \(i\) da população, a variável \(y\) é definida como:
\[ \displaystyle y_i = I(i \in A) = \begin{cases} 1, \text { se a unidade} \textit{ i } \text{possui o atributo de interesse} \\ 0, \text{ caso contrário} \end{cases} \tag{5.1} \]
O total populacional da variável \(y\) coincide com a contagem do número de unidades populacionais que possuem o atributo de interesse, ou que pertencem ao subconjunto \(A\), e pode ser representado como:
\[ Y = \displaystyle \sum_{i \in U} y_i = N_A \tag{5.2} \] onde \(N_A\) representa o número de unidades populacionais que possuem o atributo de interesse.
Um exemplo clássico do uso de variáveis indicadoras ocorre quando se quer tabular frequências de respostas a uma pergunta categórica numa pesquisa ou censo. Considere uma pergunta cujas respostas podem ser um dos valores inteiros de \(1\) a \(C\), onde \(C\) representa o número de categorias de resposta da pergunta. Por exemplo, para a pergunta ‘Qual é o sexo do morador’, há duas categorias de resposta \((C= 2)\): 1 (=Feminino) e 2 (=Masculino). Logo, para contar o número de pessoas por sexo na população, seria necessário criar duas variáveis indicadoras: \(y_{1i} = I[Sexo(i) = 1]\) e \(y_{2i} = I[Sexo(i) = 2]\). Estas contagens poderiam ser representadas por \(N_1\), para as pessoas do sexo Feminino, e \(N_2\), para as pessoas do sexo Masculino, que seriam obtidos como dois totais populacionais:
\[ \displaystyle Y_1 = \sum_{i \in U} y_{1i} = N_1 \\ Y_2 = \sum_{i \in U} y_{2i} = N_2 \]
Como já adiantado no Capítulo 3, quando a variável \(y\) é do tipo indicadora, a média populacional dada por:
\[ \overline {Y} = \displaystyle \frac{1}{N} \sum_{i \in U} y_i = \frac {Y}{N} = \frac {N_A} {N} = p \, \, \tag{5.3} \]
corresponde à proporção \(p\) de unidades da população que têm o atributo de interesse. O parâmetro populacional proporção é aqui representado pela letra \(p\) minúscula, já que a letra \(P\) maiúscula já foi usada para denotar probabilidade.
Uma proporção pode assumir valores variando entre \(0\), quando nenhuma unidade da população tem o atributo investigado, até \(1\), quando todas as unidades possuem esse atributo. Muitas vezes é interessante expressar a proporção sob forma de porcentagem podendo então variar de 0% até 100%.
Como \(y\) só pode receber valores \(0\) ou \(1\), a expressão da sua variância populacional pode ser simplificada:
\[ \hspace{-1.0cm} S^2_y = \displaystyle \frac {1}{N-1} \left( \sum_{i \in U} y^2_i - N \overline{Y}^2 \right) = \frac{1}{N-1} \left(Np-Np^2 \right) = \frac{N}{N-1} p \left(1-p\right) \tag{5.4} \]
A variância populacional de \(y\) pode também ser definida como \(\sigma^2_y = p (1-p)\). Tanto \(S^2_y\) como \(\sigma^2_y\) representam a dispersão da distribuição dos valores de \(y\) na população. Para populações com um grande número de unidades \((N \displaystyle \rightarrow \infty)\), é fácil verificar que as duas quantidades são praticamente iguais, pois pode-se considerar \(S^2_y \displaystyle \doteq p(1-p) = \sigma^2_y\).
Outra medida importante para avaliar a dispersão de uma variável é o seu Coeficiente de Variação ou CV, definido como a razão entre o Desvio Padrão de \(y\) e sua média:
\[ CV_y = \frac {\sqrt {\sigma^2_y}} {\overline Y} = \sqrt {{p(1-p) / p^2}} = \sqrt {(1-p)/p}\quad \tag{5.5} \]
Exemplo 5.1 Seja uma escola de ensino fundamental onde se deseja estudar a composição dos estudantes por sexo. Vamos supor que a escola tenha um total de 1.000 estudantes, dos quais 480 são do sexo feminino. Pode-se definir a variável \(y\) de interesse como: \[ \displaystyle y_i = \begin{cases} 1, \,\, \text {se o estudante for do sexo feminino} \\ 0, \,\, \text {caso contrário} \end{cases} \]
O total de meninas da escola será o total da variável \(y\), dado por: \[ Y = N_A = \displaystyle \sum_{i \in U} y_i = 1+1+0+1+...+0+1+1 = 480 \] A média da variável \(y\), que neste caso é também a proporção de meninas entre os estudantes da escola, é igual a: \[ \overline Y = \frac Y N = \frac {N_A}{N} = p = \frac {480} {1.000}=0,48 \text { ou } 48\% \]
A variância da variável \(y\), medida por \(S^2_y\) é igual a: \[ S^2_y = \frac N {N-1}p(1-p) = \frac{1.000}{999} \times 0,48 \times 0,52 \doteq 0,24985 \]
e quando medida por \(\sigma^2_y\) fica igual a \[ \sigma^2_y = p(1-p) = 0,48 \times 0,52 = 0,2496 \]
Finalmente, o coeficiente de variação de \(y\) é igual a: \[ CV_y = \sqrt {\frac {1-p}{p}} = \sqrt \frac{0,52}{0,48} \doteq 1,041 \]
Podemos obter os resultados acima utilizando um script escrito em R.
# Alunos da escola
N=1000
# Meninas
Na=480
# Proporção de meninas
(p=Na/N)## [1] 0.48# Variância
(S2y=N/(N-1)*p*(1-p))## [1] 0.2498498(Sigma2y=p*(1-p))## [1] 0.2496# Coeficiente de variação
(CVy=sqrt((1-p)/p))## [1] 1.040833Nas duas seções seguintes tratamos do problema da estimação desses parâmetros populacionais a partir dos dados de amostras aleatórias simples retiradas da população de interesse com e sem reposição, respectivamente.
5.2 Estimação sob amostragem aleatória simples com reposição
Seja \(s\) uma AASC de tamanho \(n\) selecionada de uma população composta de \(N\) unidades, onde se observa uma variável indicadora \(y\) como definida na seção anterior. Pode-se obter estimadores para os parâmetros populacionais de \(y\) adaptando os estimadores gerais de total e média apresentados no capítulo anterior.
O total de unidades da amostra com o atributo de interesse, \(n_A\), será dado pela soma amostral:
\[ t_y = \displaystyle \sum_{i \in\ s} y_i = n_A \,\, \tag{5.6} \] O total de unidades na população com o atributo de interesse, \(N_A\), é estimado usando:
\[ \widehat Y_{AASC} = N \times t_y / n = N \times n_A / n = \widehat N_A \tag{5.7} \] Como indicado no capítulo anterior, este estimador é não viciado sob AASC para qualquer variável \(y\), logo é ENV também quando \(y\) é do tipo indicadora, como aqui definido.
A proporção amostral de unidades que possuem o atributo de interesse é dada pela média amostral:
\[ \displaystyle \overline y = \frac {1}{n} \sum_{i \in s} y_i = \frac {n_A}{n} = \widehat p \,\, \tag{5.8} \]
Pode-se facilmente verificar que \(\widehat p\) é um estimador não viciado para a proporção populacional \(p\), pois:
\[ \displaystyle E_{AASC} (\widehat p) = E_{AASC} (\overline y) = \overline Y = p \,\, \tag{5.9} \]
A variância da proporção amostral sob AASC é dada por:
\[ \displaystyle V_{AASC} (\widehat p) = \frac {\sigma^2_y}{n} = \frac {p(1-p)}{n} \,\, \tag{5.10} \]
A variância amostral de \(y\) é dada por:
\[ \displaystyle \widehat S^2_y = \frac {n}{n-1} \widehat p (1 - \widehat p) \tag{5.11} \]
Sob AASC, a variância amostral \(\widehat S^2_y\) é um estimador não viciado para a variância populacional \(\sigma^2_y\). Assim se obtém um estimador não viciado para a variância do estimador \(\widehat p\) como:
\[ \displaystyle \widehat {V}_{AASC} (\widehat p) = \frac {\widehat p (1 - \widehat p)}{n-1} \,\, \tag{5.12} \] O total de unidades na população que possuem o atributo de interesse e respectivo estimador são obtidos por: \[ N_A= Np\:\:\text{e}\:\: \widehat N_A=N\widehat p \]
A variância da estimativa de \(N_A\) e seu estimador são dadas por: \[ V_{AASC}(\widehat N_A)=N^2\frac {p(1-p)} {n}\:\:\text{e}\:\:\widehat V_{AASC}(\widehat N_A)=N^2\frac {\widehat p(1- \widehat p)} {n-1} \]
A Tabela 5.1 reúne os resultados principais da estimação de contagens e proporções sob AASC.
| Estimador |
|---|
| \(\displaystyle\widehat N_A= N\times n_A/n = N\times \widehat p\) |
| \(\displaystyle\widehat{p}=\displaystyle n_A / n\) |
| \(\displaystyle \widehat S^2_y=\displaystyle\frac{n}{n-1}\widehat p (1-\widehat p)\) |
| \(\displaystyle\widehat V_{AASC}(\widehat N_A)=N^2\widehat{p}(1-\widehat{p})/(n-1)\) |
| \(\displaystyle\widehat V_{AASC}(\widehat{p})=\widehat{p} (1-\widehat{p})/(n-1)\) |
5.3 Estimação sob amostragem aleatória simples sem reposição
No caso de uma amostra \(s\) obtida por seleção do tipo AAS, as expressões da soma amostral \(t_y\), da proporção amostral \(\widehat p\) e da variância amostral \(\widehat S^2_y\) têm a mesma forma já apresentada acima para amostras obtidas por AASC. Em consequência, também são idênticos os estimadores para o total populacional \(N_A\) e a proporção populacional \(p\). Entretanto, uma diferença é que no caso da AAS a variância amostral \(\widehat S^2_y\) é um estimador não viciado para \(S^2_y\) e não para \(\sigma^2_y\). Também são diferentes as expressões para as variâncias dos estimadores amostrais e seus correspondentes estimadores não viciados.
Foi visto no Capítulo 4 que as variâncias dos estimadores do total e da média são dadas pelas expressões:
\[ V_{AAS} (\widehat Y) = N^2 \left( \frac 1 n - \frac {1}{N} \right) {S^2_y} \,\, \tag{5.13} \]
\[ V_{AAS} (\overline y) = \left( \frac 1 n - \frac {1}{N} \right) {S^2_y} \,\, \tag{5.14} \]
Então, no caso de variáveis \(y\) do tipo indicadoras, tem-se que as variâncias do estimador do total e da proporção populacionais são dadas por:
\[ V_{AAS} (\widehat {N} _A) = N^2 \left( \frac 1 n - \frac {1}{N} \right) \frac{N}{N-1} p(1-p) \,\, \tag{5.15} \]
\[ V_{AAS} (\widehat p) = \left( \frac 1 n - \frac {1}{N} \right) \frac{N}{N-1} p(1-p) \,\, \tag{5.16} \]
Note que para populações onde o número de unidades \(N\) é suficientemente grande, tem-se que \(V_{AAS} (\widehat p) \doteq \displaystyle\frac {p (1 - p)}{n}\), resultando numa equivalência aproximada entre os desempenhos da AAS e da AASC na estimação da proporção populacional. Intuitivamente, isso ocorre porque a probabilidade de seleção repetida sob AASC tende a ser muito pequena no caso de populações muito grandes.
Utilizando \(\widehat S^2_y\) como estimador não viciado para \(S^2_y\) chega-se aos estimadores para as variâncias dos estimadores de total e proporção:
\[ \widehat V_{AAS} (\widehat {N} _A) = N^2 \left( \frac 1 n - \frac {1}{N} \right) \frac {n\widehat p (1 - \widehat p)} {n-1} \,\,\tag{5.17} \]
\[ \widehat V_{AAS} (\widehat p) = \left( \frac 1 n - \frac {1}{N} \right) \frac {n\widehat p (1 - \widehat p)} {n-1} \,\,\tag{5.18} \]
A Tabela 5.2 reúne os resultados principais da estimação de contagens e proporções sob AAS.
| Estimador |
|---|
| \(\displaystyle\widehat N_A = N \times n_A / n = N \times\widehat p\) |
| \(\displaystyle\widehat{p} = n_A/n\) |
| \(\displaystyle \widehat S^2_y =\displaystyle\frac{n}{n-1} \widehat p (1 - \widehat p)\) |
| \(\displaystyle\widehat V_{AAS}(\widehat N_A)=N^2\left(\frac 1 n-\frac {1}{N}\right)\frac{n\widehat p (1-\widehat p)}{n-1}\) |
| \(\displaystyle\widehat V_{AAS}(\widehat p)=\left(\frac 1 n-\frac{1}{N}\right)\frac{n\widehat p(1-\widehat p)} {n-1}\) |
5.4 Distribuição amostral exata de estimadores de proporção sob AASC e AAS
Na AASC, as unidades amostrais são selecionadas com igual probabilidade e com reposição a cada sorteio. Então as variáveis aleatórias \(Y_k\), que correspondem aos valores observados na amostra a cada sorteio \(k\), \(k=1, \dots, n\), são independentes e identicamente distribuídas com probabilidades definidas por:
\[ \hspace{-1.0cm} \begin{align} \displaystyle P(Y_k = 1) = P(y_{i_k} \text{ ter o atributo de interesse}) = \frac {N_A} {N} = p \\ P(Y_k = 0) = P(y_{i_k} \text{ não ter o atributo de interesse}) = 1 - \frac {N_A} {N} = 1-p \end{align}\,\, \tag{5.19} \]
Dessa maneira fica configurada uma distribuição de \(\text {Bernoulli}(p)\) para cada uma dessas variáveis: \[ \begin{array}{c | c c} {v} & \ 1 & 0 \\ \hline \text{$P(Y_k = v)$} & p & 1-p \\ \end{array} \] Ainda sob AASC, a soma amostral \(t_y = n_A\), que representa o número de unidades na amostra com o atributo de interesse, é então dada pela soma de \(n\) variáveis aleatórias IID com distribuição \(\text {Bernoulli}(p)\). Portanto, sob AASC a variável aleatória \(t_y = n_A\) segue uma distribuição \(\text {Binomial}(n,p)\). Imediatamente tem-se que:
\[ E_{AASC}(n_A) = n p {\quad \text e \quad} V_{AASC}(n_A) = n p (1-p) \,\, \tag{5.20} \]
Seguindo o mesmo raciocínio, pode-se ter o valor esperado e a variância de \(\widehat p\):
\[ \displaystyle E_{AASC} (\widehat p) = E_{AASC} \left(\frac{n_A}{n}\right) = p {\quad\text e \quad} V_{AASC}(\widehat p) = \frac {p (1-p)} {n} \,\, \tag{5.21} \]
Outro resultado importante é que nesse caso se pode obter a distribuição de probabilidades exata de \(\widehat p\), pois:
\[ \hspace{-0,4cm} \displaystyle P \left(\widehat p = \frac v n \right) = P(n_A = v) = \binom{n} {v} p^v (1-p)^{n-v} ,\quad \forall\, v=0, 1, 2, ..., n \tag{5.22} \]
Esta distribuição corresponde apenas a uma transformação escalar da distribuição \(\text {Binomial}(n,p)\), onde a contagem de sucessos \((n_A)\) é dividida pelo número de sorteios \((n)\).
Sob AAS, a distribuição da contagem de sucessos \((n_A)\) tem uma distribuição de probabilidades \(\text {Hipergeométrica}(N, N_A, n)\). Isso ocorre porque, sob AAS, os \(n\) sorteios são feitos da população sem reposição e, portanto, a cada nova unidade sorteada, o número de unidades remanescentes na população com o atributo de interesse varia, dependendo do número dessas unidades já selecionadas.
O número total de amostras aleatórias simples sem reposição de tamanho \(n\) que podem ser selecionadas de uma população com \(N\) unidades é dado por \(\binom{N}{n}\); o número dessas amostras com exatamente \(v\) unidades com a característica em estudo e \(n-v\) unidades sem essa característica pode ser calculado por \(\binom{N_A}{v}\binom{N-N_A}{n-v}\). Sendo assim, a distribuição de probabilidades da variável aleatória \(t_y = n_A\) é dada por:
\[ \displaystyle P \left(n_A = v \right) = \frac {\binom{N_A} {v} \binom{N-N_A} {n-v}}{\binom{N} {n}} , \quad \forall\, v=0, 1, 2, ..., min(n;N_A) \,\, \tag{5.23} \]
e assim fica também determinada a distribuição exata de probabilidades do estimador \(\widehat p\), que é a mesma de \(n_A\) com os valores possíveis divididos pelo tamanho da amostra \(n\).
Consequentemente tem-se que o valor esperado de unidades com o atributo de interesse na amostra e sua variância serão dados por:
\[ \displaystyle E_{AAS}(n_A)=n\frac{N_A}N=np \quad\text e\quad V_{AAS}(n_A)=np(1-p)\frac{N-n}{N-1} \,\, \tag{5.24} \]
Para o estimador, \(\widehat p=n_A/n\), da proporção de unidades com o atributo de interesse na população tem-se:
\[ \displaystyle E_{AAS}(\widehat p)=p \quad\text e\quad V_{AAS}(\widehat p)=\left(\frac1n-\frac1N\right)S^2_y\,\, \tag{5.25} \]
5.5 Intervalos de confiança para proporções na amostragem aleatória simples
Foi visto que na Amostragem Aleatória Simples, tanto com ou sem reposição, são conhecidas as distribuições exatas para o estimador \(\widehat p\). Portanto, é possível obter os limites inferior e superior para intervalos de confiança para a proporção \(p\), com um nível de significância \(\alpha\) fixado. Para isso, no caso de AASC, é necessário resolver o sistema de equações determinando os valores de \(\widehat p_I\) e \(\widehat p_S\) que satisfaçam:
\[ \begin{cases} \displaystyle \sum _{v=0}^{n_A} \binom {n}{v} \widehat p_S^v (1 - \widehat p_S)^{n-v} = \alpha / 2 \\\\ \displaystyle \sum _{v=n_A}^n \binom {n}{v} \widehat p_I^v (1 - \widehat p_I)^{n-v} = \alpha / 2 \tag{5.26} \end{cases} \] No caso da AAS, o sistema a ser resolvido é baseado na distribuição Hipergeométrica como se segue:
\[ \begin{cases} \displaystyle \sum_ {v=0}^{n_A}\frac {\binom{N\widehat p_S}{v} \binom{N-N\widehat p_S} {n-v}}{\binom{N}{n}} = \alpha / 2 \\\\ \displaystyle \sum_ {v=n_A}^{n}\frac {\binom{N\widehat p_I}{v} \binom{N - N \widehat p_I} {n-v}} {\binom{N}{n}} = \alpha / 2 \tag{5.27} \end{cases} \]
Em ambos os casos \(1 - \alpha\) é o nível de confiança desejado. Por exemplo, para intervalos de 95% de confiança, deve-se usar \(\alpha= 0,05\).
A solução desses sistemas costumava ser trabalhosa, exigindo aplicação de métodos iterativos que consumiam quantidade razoavelmente grande de recursos computacionais. Atualmente, com o avanço dos métodos computacionais, esse problema pode facilmente ser resolvido, por exemplo, com o uso do R. Uma maneira é utilizar as funções qbinom e qhyper que podem calcular os quantis das distribuições Binomial e Hipergeométrica para \(\alpha /2\) e \(1 -\alpha /2\).
Além disso, há outros programas prontos facilmente utilizávies como, por exemplo, as funções binconf e confCI incluídas, respectivamente, nos pacotes Hmisc e prevalence do R. Essas funções estimam intervalos de confiança para vários métodos além do mostrado acima, como o da aproximação Normal, apresentado na próxima seção, além de outras abordagens. Há, também, no pacote survey uma função específica, svyciprop, para calcular intervalos de confiança para proporções. Uma característica interessante do pacote survey é que é possível determinar a utilização do fator de correção para populações finitas, quando a seleção é sem reposição.
Exemplo 5.2 Voltando ao exemplo da escola com \(N=1.000\) alunos, suponha que foi selecionada uma amostra aleatória simples de tamanho \(n=125\) e foi investigado o sexo de cada um desses alunos, sendo que 60 são do sexo feminino. Construir um intervalo de aproximadamente 95% de confiança para a proporção de alunos do sexo feminino, utilizando os vários métodos da linguagem R sugeridos acima.
# Carregando pacotes necessários
suppressMessages(require(Hmisc, quietly=TRUE,warn.conflicts=FALSE,character.only=FALSE))## Warning: package 'Hmisc' was built under R version 4.1.2## Warning: package 'ggplot2' was built under R version 4.1.2suppressMessages(require(survey, quietly=TRUE,warn.conflicts=FALSE,character.only=FALSE))
suppressMessages(require(prevalence,quietly=TRUE,warn.conflicts=FALSE,character.only=FALSE))## Warning: package 'prevalence' was built under R version 4.1.2## Warning: package 'rjags' was built under R version 4.1.2## Warning: package 'coda' was built under R version 4.1.2 # Definição do arquivo da amostra para a função svyciprop
s=as.data.frame(c(rep(1,60),rep(0,125-60)))
names(s)=c("y")
s$N=1000 # tamanho da população (número de alunos da escola)
s$n=dim(s)[1] # tamanho da amostra
s$x=sum(s$y) # mulheres na amostra
s$peso=s$N/s$n # pesos amostrais (inverso da fração amostral)
# Parâmetros de entrada para outras funções
N=s$N[1]
n=s$n[1]
x=s$x[1]
p=x/n
alfa = 0.05 # nível de significância
# Caso a amostra tenha sido selecionada com reposição
# Usando a função qbinom
c=c(p,qbinom(alfa/2,n,p)/n,qbinom(1-alfa/2,n,p)/n)
names(c)=c("p","li","ls")
# Intervalo de confiança
c## p li ls
## 0.480 0.392 0.568# Usando a função binconf
binconf(x,n,method="all",alpha=alfa)## PointEst Lower Upper
## Exact 0.48 0.3898361 0.5711333
## Wilson 0.48 0.3943277 0.5668649
## Asymptotic 0.48 0.3924179 0.5675821 # Usando a função propCI
propCI(x,n,method="all",level=1-alfa)## x n p method level lower upper
## 1 60 125 0.48 agresti.coull 0.95 0.3943257 0.5668669
## 2 60 125 0.48 exact 0.95 0.3898361 0.5711333
## 3 60 125 0.48 jeffreys 0.95 0.3937144 0.5671999
## 4 60 125 0.48 wald 0.95 0.3924179 0.5675821
## 5 60 125 0.48 wilson 0.95 0.3943277 0.5668649 # Usando a função svyciprop
desaasc=svydesign(ids=~1,data=s,weights=~peso, fpc=NULL) # plano amostral de AASC (sem FPC)
svyciprop(~I(y==1),desaasc,method="logit")## 2.5% 97.5%
## I(y == 1) 0.480 0.393 0.57svyciprop(~I(y==1),desaasc,method="likelihood")## 2.5% 97.5%
## I(y == 1) 0.480 0.392 0.57svyciprop(~I(y==1),desaasc,method="asin")## 2.5% 97.5%
## I(y == 1) 0.480 0.392 0.57svyciprop(~I(y==1),desaasc,method="beta")## 2.5% 97.5%
## I(y == 1) 0.480 0.389 0.57svyciprop(~I(y==1),desaasc,method="mean")## 2.5% 97.5%
## I(y == 1) 0.480 0.391 0.57svyciprop(~I(y==1),desaasc,method="xlogit")## 2.5% 97.5%
## I(y == 1) 0.480 0.393 0.57 # Caso a amostra tenha sido selecionada sem reposição
# Usando a função qhyper
li=qhyper(alfa/2,N*p,N-N*p,n)/n
ls=qhyper(1-alfa/2,N*p,N-N*p,n)/n
c(p,li,ls)## [1] 0.48 0.40 0.56 # Usando a função svyciprop
desaas=svydesign(ids=~1,data=s,weights=~peso,fpc=~N) # plano amostral de AAS (com FPC)
svyciprop(~I(y==1),desaas,method="logit")## 2.5% 97.5%
## I(y == 1) 0.480 0.398 0.56svyciprop(~I(y==1),desaas,method="likelihood")## 2.5% 97.5%
## I(y == 1) 0.480 0.398 0.56svyciprop(~I(y==1),desaas,method="asin")## 2.5% 97.5%
## I(y == 1) 0.480 0.398 0.56svyciprop(~I(y==1),desaas,method="beta")## 2.5% 97.5%
## I(y == 1) 0.480 0.395 0.57svyciprop(~I(y==1),desaas,method="mean")## 2.5% 97.5%
## I(y == 1) 0.480 0.397 0.56svyciprop(~I(y==1),desaas,method="xlogit")## 2.5% 97.5%
## I(y == 1) 0.480 0.398 0.56Na função binconf o método denominado Exact utiliza uma aproximação da Binomial pela distribuição F; o método denominado Wilson é baseado nos scores do teste binomial e é o método definido como default por ser considerado o melhor; já o método denominado Asymptotic é o da aproximação pela distribuição Normal.
Na função propCI são apresentados outros dois métodos: O método Agresti-Coull que é um ajuste da aproximação Normal e o método Jeffreys que é um método Bayesiano. O método Asymptotic é chamado de Wald.
Para as duas funções acima não se considera se a amostra foi selecionada com ou sem reposição, o que é perfeitamente aceitável para amostras grandes retiradas de populações também grandes.
Para a função svyciprop, do pacote survey, é possível definir se a amostra foi selecionada sem ou com reposição, bastando fornecer, ou não, o tamanho, \(N\), da população para o cálculo do fator de correção para população finita. Nessa função é possível escolher entre 6 possíveis métodos para o cálculo do intervalo de confiança.
Para detalhes sobre estas e demais funções do R, ver R Core Team (2018). Para um pacote específico, pode-se obter uma referência mais completa digitando, no próprio R, o comando citation(‘nome do pacote’).
Pode-se observar que, nos exemplos acima, onde o tamanho da amostra é grande, os resultados de todos os métodos utilizados, em termos práticos, são bastante parecidos. Fica como exercício para o leitor verificar o que acontece quando for utilizada uma amostra de tamanho pequeno (menor que 30, por exemplo).
Na maioria dos casos práticos, opta-se pelo uso da aproximação pela distribuição Normal de probabilidades, pela facilidade de seu uso tanto para AAS como AASC. Isso pode ser feito sempre que as condições do problema assim o permitirem, como se discute na próxima seção.
5.6 Intervalos de confiança utilizando a aproximação Normal
Como já foi visto no capítulo anterior, a distribuição do estimador da proporção, \(\widehat p\), pode ser aproximada pela distribuição Normal de probabilidade. Esta aproximação pode ser utilizada mesmo no caso da AAS onde os \(y_i\) observados na amostra não são independentes, desde que se tenha valores de \(N\) e \(n\) suficientemente grandes e valor da fração amostral, \(f=\frac n N\), pequeno.
Sob estas condições pode-se considerar que:
\[ \frac {\widehat p - p} {\sqrt {V_{p(s)}(\widehat p)}} \approx N(0;1)\tag{5.28} \]
A Figura 5.1 mostra o histograma construído a partir dos valores estimados da proporção \(p\) de unidades com uma determinada característica de interesse, a partir de 1.000 amostras aleatórias simples de tamanho \(n=100\), selecionadas com reposição, de uma população de tamanho \(N=5.000\), onde exatamente metade das unidades tem a característica de interesse \((p=1/2)\). Para construir o histograma, os 1.000 valores de \(\widehat p\) foram normalizados utilizando-se a Expressão (5.28). Finalmente o histograma foi sobreposto pelo gráfico da distribuição \(N(0;1)\), mostrando que esta se assemelha à distribuição do estimador \(\widehat p\).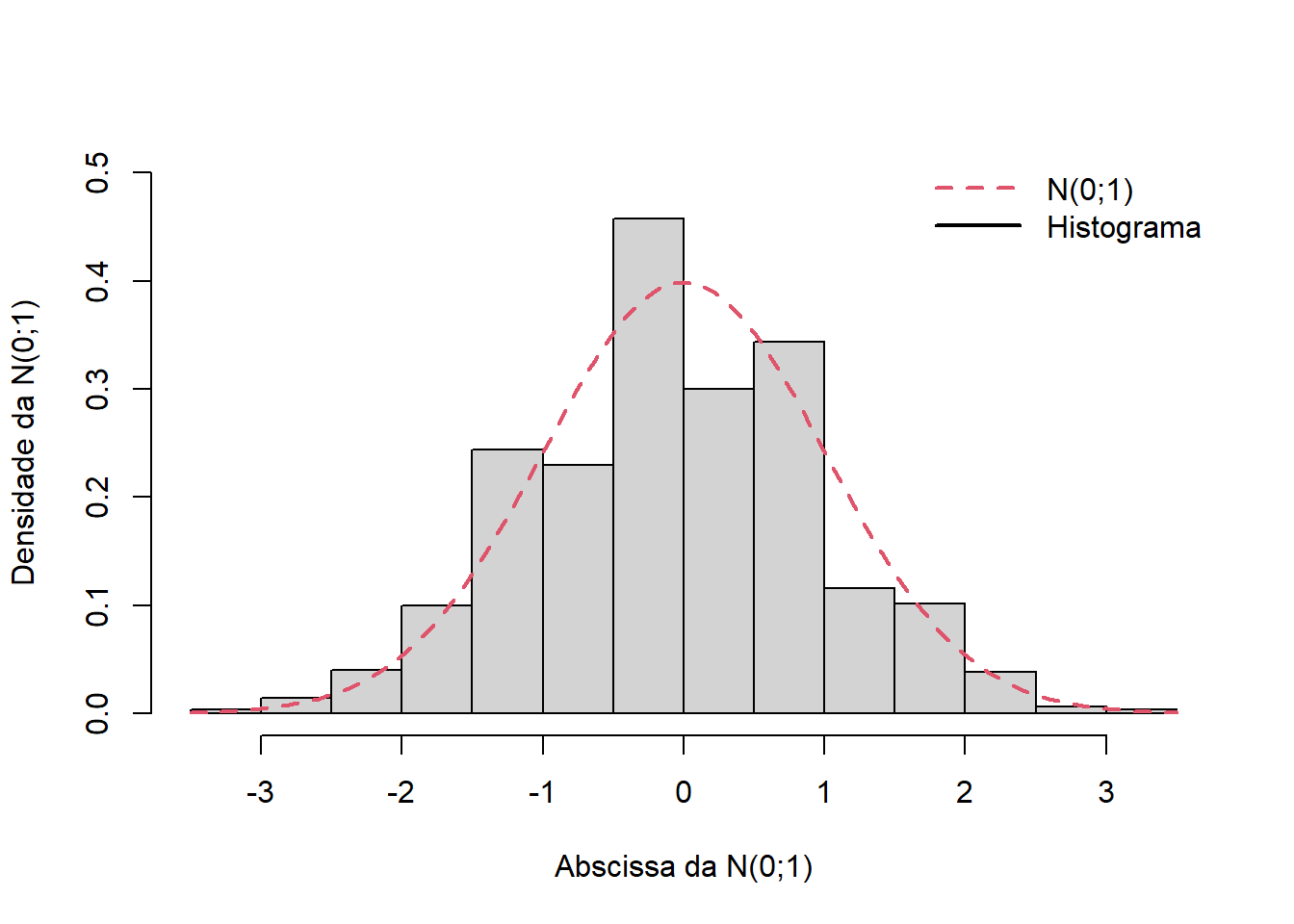
Figura 5.1: Aproximação Normal da distribuição do estimador de \(p\) no caso de AASC
A Figura 5.2 mostra o gráfico para um exercício similar ao anterior onde as amostras foram selecionadas sem reposição.
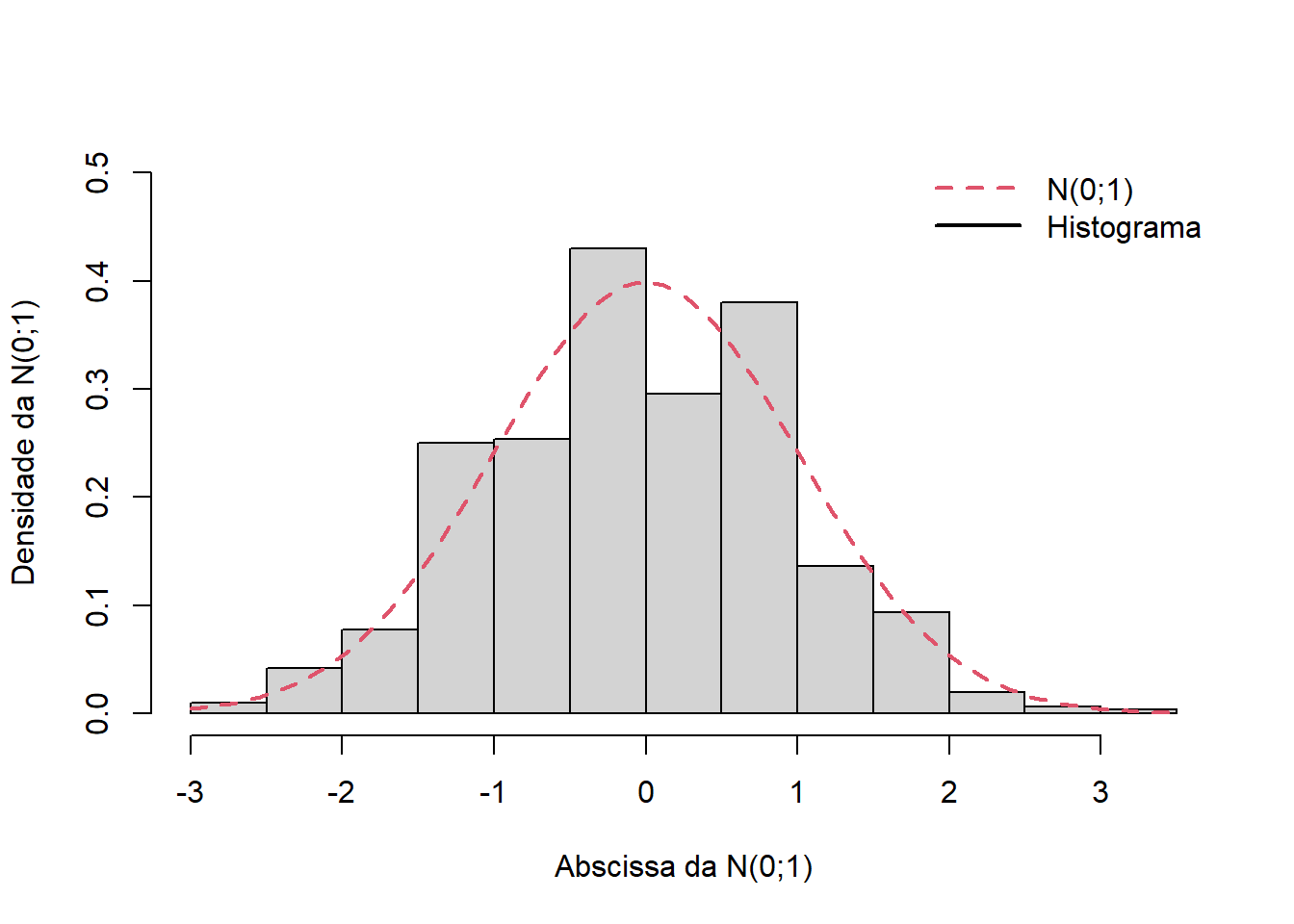
Figura 5.2: Aproximação Normal da distribuição do estimador de \(p\) no caso de AAS
Tanto nos casos de seleção com ou sem reposição pode-se considerar que as aproximações são satisfatórias, com os histogramas das distribuições amostrais do estimador \(\widehat p\) aderindo consideravelmente à curva Normal padrão.
Cochran (1977) mostra uma tabela, reproduzida na Tabela 5.3, com alguns valores mínimos do total de unidades observadas na amostra, \(n_A\), onde a aproximação Normal pode ser utilizada.
| \(p\) | \(n_A\) | \(n\) | |
|---|---|---|---|
| 0,50 | 15 | 30 | |
| 0,40 | 20 | 50 | |
| 0,30 | 24 | 80 | |
| 0,20 | 40 | 200 | |
| 0,10 | 60 | 600 | |
| 0,05 | 70 | 1.400 | |
| \(\doteq 0\) | 80 | \(\infty\) |
A Tabela 5.3 foi construída considerando um nível de significância de \(\alpha=0,05\), que é um valor comumente utilizado em muitas situações práticas.Tem-se, a partir daí, critérios práticos para assumir a utilização da aproximação Normal, notando-se que o tamanho mínimo da amostra requerido é de \(n=30\small.\)
Nas condições estabelecidas para a validade da aproximação Normal, tem-se que \(S^2_y \doteq \sigma^2_y=p(1-p)\), portanto, \(\displaystyle V_{AAS}(\widehat p) \doteq V_{AASC}(\widehat p)\). Então, para os dois tipos de seleção, pode-se considerar o intervalo de confiança para a proporção como:
\[ \displaystyle IC(p;{1-\alpha})=\left[\widehat p-z_{\alpha/ 2}\sqrt { \frac{p(1-p)}n}\,;\,\widehat p+z_{\alpha/2}\sqrt {\frac{p(1-p)}n}\,\, \right]\,\,\tag{5.29} \] Caso se deseje considerar o fator de correção para populacões finitas, quando a fração amostral não possa ser considerada pequena e a seleção for sem reposição, a expressão do intervalo de confiança passa a ser:
\[ \displaystyle IC(p;{1-\alpha})=\left[\widehat p \mp z_{\alpha/ 2}\sqrt { \left(\frac{N-n}{N-1} \right)\frac{p(1-p)}{n}}\ \right]\,\,\tag{5.30} \]
Em Cochran (1977) é apresentada uma correção de continuidade acrescentando a fração \(1/2n\) à margem de erro do intervalo de confiança pelo fato de se fazer uma aproximação de uma distribuição discreta (Binomial ou Hipergeométrica) pela distribuição Normal, que é contínua. Desse modo a expressão do intervalo de confiança passa a ser:
\[ \displaystyle IC(p;{1-\alpha})=\left[\widehat p \mp \left(z_{\alpha/ 2}\sqrt {\frac{p(1-p)}n}+\frac1{2n} \right) \right] \tag{5.31} \] Ou considerando a correção para população finita:
\[ \displaystyle IC(p;{1-\alpha})=\left[\widehat p \mp \left(z_{\alpha/ 2}\sqrt { \left(\frac {N-n}{N-1} \right) \frac{p(1-p)}{n}}+\frac 1 {2n} \right) \right]\tag{5.32} \]
Nas aplicações práticas o valor da variância do estimador da proporção \(p\), geralmente, não é conhecido. Assim o que se pode fazer é estimar um intervalo de confiança, substituindo \(S^2_y\) por \(\widehat S^2_y\) na expressões anteriores:
\[ \displaystyle \widehat{IC}(p;{1-\alpha})=\left[\widehat p \mp \left(z_{\alpha/ 2}\sqrt {\frac{\widehat p \widehat q} {n-1}} + \frac 1{2n} \right) \right]\tag{5.33} \]
\[ \displaystyle \widehat{IC}(p;{1-\alpha})=\left[\widehat p \mp \left(z_{\alpha/ 2}\sqrt {\left(\frac{N-n}{N}\right) \frac{\widehat p \widehat q} {n-1}} + \frac 1{2n} \right) \right]\tag{5.34} \]
Note que o efeito da correção de continuidade tende rapidamente a ser nulo quando o tamanho da amostra, \(n\), cresce. Para uma amostra de tamanho \(n=50\) esse fator já é de apenas 1%, o que pode ser desprezível dependendo da proporção que estiver sendo estimada, porém é preciso muito cuidado pois quando se está trabalhando com proporções são valores, às vezes, bastante pequenos.
Exemplo 5.3 Em um período pré-eleitoral, deseja-se estimar a intenção de votação dos eleitores nos candidatos A e B. Para isso foi selecionada e pesquisada uma amostra AAS de 2.000 eleitores. Desses, 900 declararam intenção de votar em A, 800 em B e os demais 300 se disseram indecisos. Supondo que o total de eleitores da população de pesquisa é de 4 milhões, responda às perguntas abaixo.
- Qual a proporção e quantos eleitores planejam votar em A? Obtenha o IC de 95% para os valores populacionais.
- Repita para o candidato B.
- Estime a proporção e o número de indecisos e os correspondentes IC de 95%.
Para responder essas questões, pede-se utilizar o R.
# Opção para controlar impressão de valores grandes e evitar uso de notação científica
options(scipen=8)
# Tamanho populacional
(N <- 4000000)## [1] 4000000# Tamanho amostral
(n <- 2000)## [1] 2000# Eleitores dos candidatos na amostra
(n_A <- 900) # Candidato A## [1] 900(n_B <- 800) # Candidato B## [1] 800(n_I <- 300) # Indecisos## [1] 300# Estimativa da proporção e de número de eleitores de A
(p_A <- (n_A / n))## [1] 0.45(N_A <- N*p_A)## [1] 1800000# Estimativa da proporção e do número de eleitores de B
(p_B <- (n_B / n))## [1] 0.4(N_B <- N*p_B)## [1] 1600000# Estimativa da proporção e número de eleitores Indecisos
(p_I <- (n_I / n))## [1] 0.15(N_I <- N*p_I)## [1] 600000# Intervalos de confiança, com aproximação Normal, para o candidato A
(me_P_A <- qnorm(0.975)*sqrt(p_A*(1-p_A)/n))## [1] 0.02180322(LIC_P_A <- p_A - me_P_A)## [1] 0.4281968(LSC_P_A <- p_A + me_P_A)## [1] 0.4718032(LIC_N_A <- N*LIC_P_A)## [1] 1712787(LSC_N_A <- N*LSC_P_A)## [1] 1887213# Intervalos de confiança, com aproximação Normal, para o candidato B
(me_P_B <- qnorm(0.975)*sqrt(p_B*(1-p_B)/n))## [1] 0.02147033(LIC_P_B <- p_B - me_P_B)## [1] 0.3785297(LSC_P_B <- p_B + me_P_B)## [1] 0.4214703(LIC_N_B <- N*LIC_P_B)## [1] 1514119(LSC_N_B <- N*LSC_P_B)## [1] 1685881# Intervalos de confiança, com aproximação Normal, para os indecisos
(me_P_I <- qnorm(0.975)*sqrt(p_I*(1-p_I)/n))## [1] 0.01564906(LIC_P_I <- p_I - me_P_I)## [1] 0.1343509(LSC_P_I <- p_I + me_P_I)## [1] 0.1656491(LIC_N_I <- N*LIC_P_I)## [1] 537403.8(LSC_N_I <- N*LSC_P_I)## [1] 662596.25.7 Cálculo do tamanho da amostra
O tamanho de uma amostra aleatória simples a ser selecionada, como já foi visto no capítulo anterior, é calculado a partir da definição do erro amostral ou margem de erro admissível para o caso, do nível de confiança desejado e se a seleção for com ou sem reposição.
No caso de seleção com reposição, considerando uma margem de erro máxima admissível \(D\) com um nível de confiança \(1-\alpha\), basta utilizar a expressão da margem de erro:
\[ D \le z_{\alpha/2}\sqrt { \frac{p(1-p)}{n}} \implies n \ge \frac{z^2_{\alpha/2}{p(1-p)}}{D^2} \tag{5.35} \] Para a seleção sem reposição, o tamanho da amostra é calculado como:
\[ \hspace{-2,0cm} D \le z_{\alpha/2}\sqrt{\left(\frac {N-n}{N-1}\right)\frac{p(1-p)}n} \implies n \ge \frac{z^2_{\alpha/2}p(1-p)} {D^2 \frac {N-1}N + \frac 1 N {z^2_{\alpha /2}p(1-p)}} \] Considerando \(\displaystyle\frac{N-1}{N}\doteq 1\), tem-se que:
\[ \hspace{-2,0cm} D \le z_{\alpha/2}\sqrt{\left(\frac {N-n}{N-1}\right)\frac{p(1-p)}n} \implies n \ge \frac {Np(1-p)}{ND^2 /{z^2_{\alpha /2}} + p(1-p)} \tag{5.36} \]
Uma maneira prática de calcular o tamanho da amostra para uma AAS em dois passos é calcular primeiro:
\[ n_0=\frac{z^2_{\alpha/2}p(1-p)}{D^2}\tag{5.37} \] E depois fazer:
\[ n \ge \frac {n_0}{1+n_0 /N}\tag{5.38} \]
Note que \(n_0\) é equivalente ao tamanho da amostra para uma AASC e o valor de \(n\) para a AAS é obtido pela correção para população finita do valor \(n_0\). Também pode-se concluir que quando o tamanho da população, \(N\), é grande o fator \(n_0/N\) tende a se anular fazendo com que \(n \doteq n_0\), ou seja, quando o tamanho da população é grande as amostras aleatórias simples com ou sem reposição são equivalentes.
As fórmulas apresentadas dependem do nivel de significância \(\alpha\) e da margem de erro \(D\) que devem ser definidos pelo pesquisador de acordo com seu conhecimento relativo ao assunto pesquisado, pois esses valores estão diretamente ligados à natureza da pesquisa.
Pesquisas que utilizam medidas objetivas para alcançar seus resultados, como instrumentos para medir fisicamente o fenômeno estudado, podem ser mais exigentes quanto à precisão das estimativas desejadas, enquanto que pesquisas da área social, por exemplo, onde se utilizam questionários e que dependem da memória ou até da boa vontade dos entrevistados, frequentemente não podem ter o mesmo nível de exigência.
O tamanho da amostra também depende da variância da variável utilizada para seu cálculo, através do produto \(p(1-p)\). Como \(p\) é a proporção que se deseja estimar, se fosse conhecida não haveria a necessidade de uma amostra. Geralmente, como no caso de se pesquisar variáveis contínuas, utilizam-se pesquisas anteriores ou variáveis correlacionadas com a atual variável de interesse, ou mesmo uma pesquisa piloto com um tamanho arbitrário de amostra, para se ter uma estimativa inicial do fenômeno a ser medido e poder calcular o tamanho de amostra realmente necessário. Quando se utiliza uma pesquisa piloto, existem métodos para utilizar os resultados relativos às unidades já pesquisadas e selecionar outras unidades para complementar o tamanho da amostra.
No caso da estimação de proporções, o valor de \(p(1-p)\) é limitado variando de 0 a 0,25, sendo esse valor máximo atingido quando \(p= 0,5\). O gráfico da Figura 5.3 mostra como variam os valores de \(p(1-p)\) conforme a variação dos valores de \(p\).
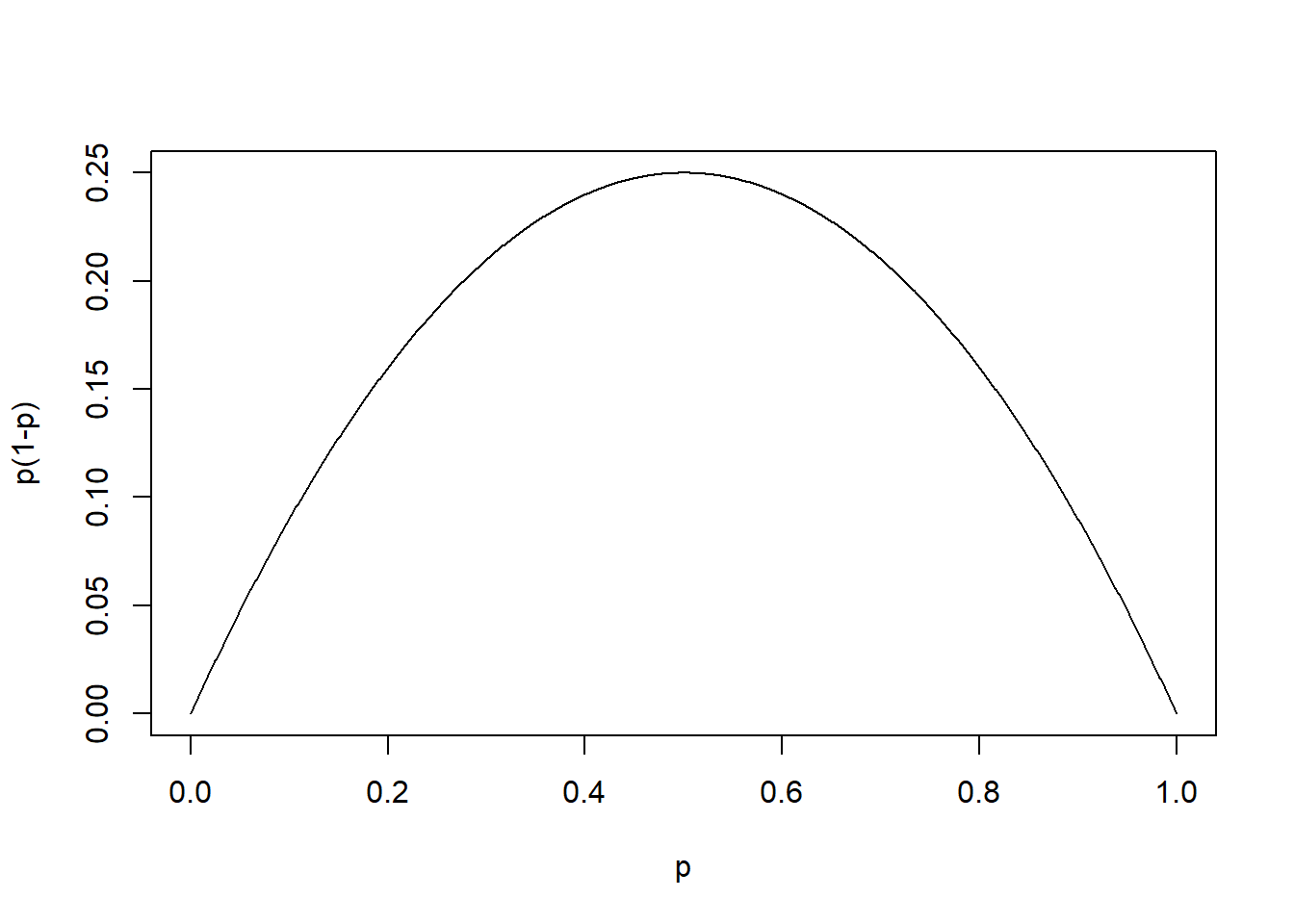
Figura 5.3: Variação de \(p(1-p)\) em função dos valores de \(p\)
Como o valor máximo de \(S_y^2\doteq \sigma _y^2=p(1-p)\), que é a maior variabilidade da variável de interesse, é atingido quando \(p=0,5\), caso não exista nenhuma informação sobre o a proporção a ser estimada, uma maneira de determinar um tamanho de amostra conservador é supor exatamente que \(p=0,5\). Assim pode-se simplificar a fórmula de cálculo de \(n\) para uma AASC:
\[ n \ge \frac {z^2_{\alpha /2}}{4D^2}\tag{5.39} \] No caso de uma AAS basta fazer:
\[ n_0 = \frac {z^2_{\alpha /2}}{4D^2} \:\:\:\:\text{e}\:\:\:\:n \ge \frac {n_0}{1+n_0/N}\tag{5.40} \]
Geralmente os resultados das fórmulas para cálculo do tamanho da amostra não são valores inteiros. Em todos esses casos o valor de \(n\) calculado deverá ser arredondado para o valor inteiro imediatamente superior, preservando assim a precisão desejada.
Exemplo 5.4 Uma empresa precisa selecionar uma amostra de uma população composta de 30.000 domicílios para estimar a proporção de domicílios que consomem suprimentos para animais domésticos. O diretor da empresa pergunta ao estatístico qual o tamanho de amostra que deve utilizar na pesquisa e diz que lhe foi sugerida a seguinte fórmula para determinar o tamanho da amostra: \[n\ge\frac {Np(1-p)}{ND^2 /{z^2_{\alpha /2}} + p(1-p)}\]
- A fórmula acima está correta? Sob que hipóteses ou condições? Se não, qual seria a fórmula correta?
- Que tamanho deveria ter a amostra para estimar a proporção de domicílios que consomem suprimentos para animais domésticos, tal que a estimativa não se afaste do verdadeiro valor da proporção mais do que 1% com 95% de confiança?
- Se o diretor da empresa informar ao estatístico que a proporção de domicílios que consomem suprimentos para animais domésticos varia no intervalo [0,10; 0,30], mudaria a resposta para o item b? Caso afirmativo, qual seria a nova resposta?
A resposta para o item a é que a fórmula está correta, pois, sendo a população bastante grande, \(N=30.000\), pode-se desprezar o fator de correção \((N-1)/N\) como mostrado na Expressão (5.36).
Para os demais itens pode-se recorrer ao R.
# Opção para controlar impressão de valores grandes e evitar uso de notação científica
options(scipen=8)
# Item b
# Especifica margem de erro
(D <- 0.01)## [1] 0.01# Tamanho da população
(N <- 30000)## [1] 30000# Valor da Normal para o nível de significância desejado
(z2alfa=qnorm(0.975))## [1] 1.959964# Item b
# Usando fórmula 'exata' e proporção que maximiza variância, já que
# não há informação sobre o valor de p
(p <- 1/2)## [1] 0.5(q <- 1-p)## [1] 0.5# Calculando o tamanho da amostra, arredondando o valor de n para cima
(n <- ceiling(N * p * q/(N*D^2/z2alfa^2 + p * q)))## [1] 7275#Item c - nste caso há a indicação de um intervalo que deve conter o valor da proporção
#a ser estimada. Deve-se, então, calcular os tamanhos de amostra para os limites do
#intervalo e optar pelo maior tamanho de amostra obtido, pois esse valor satisfaz a
#condição de maior exigência
# Usando fórmula 'exata' e proporção no limite inferior
(p <- 0.1)## [1] 0.1(q <- 1-p)## [1] 0.9# Calculando o tamanho da amostra, arredondando o valor de n para cima
(n <- ceiling(N * p * q/(N*D^2/z2alfa^2 + p * q)))## [1] 3101# Usando fórmula 'exata' e proporção no limite superior
(p <- 0.3)## [1] 0.3(q <- 1-p)## [1] 0.7# Calculando o tamanho da amostra,arredondando o valor de n para cima
(n <- ceiling(N * p * q/(N*D^2/z2alfa^2 + p * q)))## [1] 6358No caso de não existir nenhuma indicação sobre o valor de \(p\), como no item b do exemplo, deve-se tomar \(n=7.275\), supondo \(p=0,5\). Já no item c, deve-se optar pelo maior tamanho de amostra necessário para suprir as exigências de precisão. Neste caso, como a informação é que \(p\) deve estar no intervalo [0,10; 0,30] deve-se selecionar uma amostra de \(n=6.358\) domicílios.
Sugere-se que o leitor refaça o exercício com uma margem de erro diferente, \(D=0,03\), por exemplo, e observe o que acontece com os valores de \(n\) calculados.
5.7.1 Cálculo do \(n\) utilizando outras formas de representar o erro amostral
As fómulas apresentadas para o cálculo do tamanho da amostra utilizaram a margem de erro \(D\) como parâmetro de entrada, porém o erro amostral pode ser representado de outras maneiras. Pode-se defini-lo como o coeficiente de variação, como a variância ou como o erro relativo do estimador a ser calculado.
Para calcular um tamanho de amostra de maneira que o coeficiente de variação máximo esperado para o estimador \(\widehat p\) seja um valor fixado \(c\), pode-se utilizar a fórmula:
\[ n \ge \frac {1-p} {c^2p}\tag{5.41} \] no caso da seleção com reposição.
Para chegar a esse resultado, basta ver que \(CV_{AASC}(\widehat p)= \displaystyle\frac {\sqrt {V_{AASC}(\widehat p)}}p\) e substituir na fórmula apresentada para o cálculo de \(n\) a partir da margem de erro fixada.
Para a seleção sem reposição pode-se fazer:
\[ n_0 = \frac {1-p} {c^2p} \:\:\:\:\text{e}\:\:\:\: n \ge \frac {n_0} {1+n_0/N}\tag{5.42} \]
Seguindo o mesmo raciocínio pode-se chegar às formulas para calcular n fixando a variância máxima esperada de \(\widehat p\) em \(v\) ou o seu erro relativo máximo em \(r\).
Para a seleção com reposição tem-se:
\[ n \ge \frac {p(1-p)} {v} { \quad\text { ou } \quad} n \ge \frac {z^2_{\alpha/2}}{r^2} \frac {1-p} p \tag{5.43} \]
As expressões para a seleção sem reposição são derivadas como no caso em que foi fixado o valor máximo esperado para \(CV(\widehat p\)).
5.8 Estimação de proporções para variáveis com mais de duas categorias
Até o momento foi tratado o caso em que temos uma variável indicadora com duas categorias, definindo se uma determinada unidade na população (ou na amostra) tem ou não determinada característica de interesse. Muitas vezes temos a necessidade de definir mais de duas categorias como, por exemplo:
- Estudar a distribuição por faixas etárias de um grupo de pessoas.
- Estudar a classificação econômica das empresas de determinado país.
- Estimar a intenção de votos dos candidatos em uma eleição com mais de 2 candidatos, além das possibilidades de voto em branco ou nulo ou, ainda, eleitores indecisos.
Nesses casos, há interesse de estimar a proporção de unidades em cada uma das possíveis categorias e respectiva precisão.
Exemplo 5.5 Seja uma escola com 1.000 alunos distribuídos entre as 9 etapas do ensino fundamental como na Tabela 5.4:
| Etapa de ensino | Alunos | Proporção |
|---|---|---|
| 1° ano | 110 | 0,110 |
| 2° ano | 108 | 0,108 |
| 3° ano | 110 | 0,110 |
| 4° ano | 115 | 0,115 |
| 5° ano | 104 | 0,104 |
| 6° ano | 119 | 0,119 |
| 7° ano | 116 | 0,116 |
| 8° ano | 107 | 0,107 |
| 9° ano | 111 | 0,111 |
| Total | 1.000 | 1,000 |
Observe que, para calcular as proporções em cada uma das categorias, na verdade o que se faz é atribuir o valor \(1\) às unidades da categoria em questão e o valor \(0\) para as unidades pertencentes às demais categorias. Em outras palavras, se a variável tem \(M\) categorias é como se fossem \(M\) problemas com duas categorias.
A proporção de unidades da população pertencentes à categoria \(c\in (1, 2,.., M)\), é dada por:
\[ p_c=\frac {N_c} {N} \tag{5.44} \] 0nde \(N_c\) é o número de unidades na categoria \(c\) e \(N\) é o tamanho total da população.
Seja uma amostra aleatória simples (com ou sem reposição) de tamanho \(n\) e seja a variável indicadora \(y_i\) definida como:
\[ \displaystyle y_i= \begin{cases} 1, \text { se a unidade} \textit{ i } \text{pertence à categoria $c$} \\ 0, \text { se a unidade}\textit{ i } \text{ pertence a outra categoria} \end{cases} \tag{5.45} \]
Com tal definição pode-se ver que o número de unidades da categoria \(c\) na amostra será dado por:
\[ \displaystyle n_c=\sum_{i=1}^{n} y_i\tag{5.46} \] Um estimador para a proporção de unidades populacionais pertencentes à categoria \(c\) é dado por:
\[ \displaystyle \widehat p_c=\frac {1}{n} \sum_{i=1}^{n} y_i =\frac {n_c} {n}\tag{5.47} \] O problema foi reduzido ao caso de estimar proporções em variáveis com duas categorias. Pode-se obter, também, estimativas de precisão utilizando as mesmas ferramentas já apresentadas neste capítulo.
Muitas vezes pode-se estar interessado em estimar proporções para agrupamentos das categorias originais.
Voltando ao exemplo da escola do ensino fundamental, pode ser de interesse estudar a proporção de seus alunos que estão matriculados no primeiro segmento do ensino fundamental. Nesse caso, seriam contabilizados como pertencentes à categoria \(c\) de interesse todos os alunos do 1º até o 5º ano, para os quais \(y_c=1\), sendo \(y_c=0\) para os demais alunos da escola.
Outro caso de interesse ocorre quando, na aplicação de um questionário, por exemplo, aparecem respondentes que se recusaram a responder ou, mesmo, disseram que não sabiam a resposta. Num caso como esse, pode-se estar interessado em estimar a proporção das pessoas que responderam determinada alternativa, entre as pessoas que efetivamente responderam a pesquisa escolhendo uma das alternativas válidas. Um exemplo prático seria uma pesquisa sobre a intenção de voto numa eleição com apenas dois candidatos. Nesse caso, o entrevistado poderia responder que votará no canditato A, no candidato B, que votará nulo ou em branco, onde apenas as duas primeiras alternativas seriam consideradas como votos válidos.
Pode-se estimar a proporção para cada uma das quatro categorias iniciais ou apenas a proporção de votos válidos para cada um dos dois candidatos:
\[ \displaystyle \widehat p_A=\frac {n_A} {n_A+n_B} \quad\text { e } \quad\widehat p_B=\frac {n_B} {n_A+n_B}\tag{5.48} \]
Vale notar que em (5.48) tanto o numerador como o denominador do estimador da proporção são variáveis aleatórias, pois a população (eleitores que efetivamente vão votar num dos candidatos) é desconhecida.
5.9 Exercícios
Exercício 5.1 Uma pesquisa foi feita para estimar a proporção de domicílios de uma pequena vila que têm, pelo menos, um morador com 65 anos ou mais. A vila tem 651 domicílios dos quais foram pesquisados 60 e em 11 deles havia moradores com 65 anos ou mais.
- Estime a proporção \(p\) de domicílios na população que têm, pelo menos, um morador com 65 anos ou mais.
- Calcule a margem de erro da estimativa.
- Baseado nos resultados anteriores, quantos domicílios deveriam ser selecionados para estimar \(p\) com uma margem de erro de 0,08, com um nível de significância de 5%?
Exercício 5.2 Numa grande cidade, deseja-se estimar a proporção de habitantes que são favoráveis à instalação de uma usina térmica para geração de eletricidade numa área próxima a uma reserva biológica.
- Qual deve ser o tamanho de uma amostra aleatória para estimar essa proporção com uma margem de erro de 0,03, com um nível de confiança de 95%?
- E se o mesmo problema fosse em uma pequena comunidade de \(N=2.000\) habitantes, qual deveria ser o tamanho da amostra, com o mesmo nível de precisão?
Exercício 5.3 Supondo que o valor da variância populacional, \(S^2\), de uma determinada variável de interesse, \(y\), é o mesmo nos três casos a seguir, qual dos planos amostrais apresentados abaixo tem maior precisão para estimar uma proporção populacional? Por quê?
- AAS de tamanho 400 de uma população de 4.000.
- AAS de tamanho 30 de uma população de 300.
- AAS de tamanho 3.000 de uma população de 300.000.000.
Exercício 5.4 Foi selecionada uma AAS de 30 unidades de uma população composta por 100 unidades. Uma variável de interesse, \(y\), foi observada e os valores são: 8, 5, 2, 6, 6, 3, 8, 6, 10, 7, 15, 9, 15, 3, 5, 6, 7, 10, 14, 3, 4, 17, 10, 6, 14, 12, 7, 8, 12, 9.
- Qual o peso amostral de cada unidade da amostra?
- Usando o peso amostral, estime o total populacional de unidades onde \(y\) é maior que 9.
- Construa um intervalo de 95% de confiança para esse total populacional.
- Estime a proporção de unidades onde \(y\) é menor que 10.
- Construa um intervalo de 95% de confiança para a proporção de unidades onde \(y\) é menor que 10.
Exercício 5.5 Considere a população de \(N=338\) fazendas produtoras de cana-de-açúcar fornecida no arquivo ‘fazendas_dat.rds’. Selecione uma AAS de \(n=50\) fazendas e use esta amostra para obter a estimativa pontual, o erro padrão, o CV e o intervalo de confiança de 95%, para cada um dos seguintes parâmetros populacionais:
- Proporção de fazendas na região 1.
- Proporção de fazendas com Area maior que 100.
- Proporção de fazendas com produtividade (Quant/Area) maior que 67.
Exercício 5.6 Para o mesmo arquivo de fazendas do Exercício 5.5 considere um plano AAS e tamanhos amostrais \(n\) variando no conjunto \(\{5; 10; 20; 50; 100; 150 \}\). Imagine que há interesse em estimar dois parâmetros: proporção \(p_1\) de fazendas com Area maior que 100; proporção \(p_2\) de fazendas com produtividade (Quant/Area) maior que 67.
Para cada um dos tamanhos de amostra considerados:
- Obtenha 500 amostras por AAS da população de fazendas.
- Use cada uma destas amostras para calcular estimativas dos parâmetros de interesse.
- Use cada uma destas amostras para estimar o erro padrão das estimativas calculadas em b.
- Use as 500 estimativas pontuais obtidas para cada parâmetro para avaliar a adequação da aproximação Normal para a distribuição dos estimadores usados.
Exercício 5.7 Um partido político (cliente) encomendou a um instituto de pesquisa uma sondagem das intenções de votos dos eleitores brasileiros com relação a candidatos à eleição para a Presidência da República. O cliente deseja estimativas para as proporções de eleitores que intencionam votar em cada um dos três principais candidatos com erro não superior a 0,02 (2%), ao nível de confiança de 95%. Suponha que o instituto de pesquisa tem acesso a uma lista completa dos eleitores e seus endereços e pode usar essa lista para selecionar uma amostra aleatória simples sem reposição de eleitores para entrevistar. Qual o tamanho da amostra necessária para garantir a obtenção de resultados com a qualidade requerida pelo cliente?
Nota: Nesta questão, identifique a notação usada para representar os dados fornecidos e justifique as hipóteses e aproximações eventualmente efetuadas.
Exercício 5.8 Uma amostra aleatória simples sem reposição de 290 domicílios foi selecionada em certa cidade que possui 14.828 domicílios. Em cada domicílio da amostra, investigou-se a condição da família que o habitava, se proprietária ou locatária, e também a existência ou não de pelos menos um quarto tipo suíte (com banheiro). Os resultados obtidos são mostrados na Tabela 5.5.
| Domicílios | Próprios | Alugados |
|---|---|---|
| Com suíte | 141 | 109 |
| Sem suíte | 6 | 34 |
- Estime a proporção de domicílios alugados na região e forneça uma estimativa do CV desta proporção estimada.
- Estime a proporção de domicílios com suíte na região e forneça uma estimativa do CV desta proporção estimada.
- Estime a proporção de domicílios alugados e com suíte na região e forneça uma estimativa do CV desta proporção estimada.
Exercício 5.9 Uma AAS de 400 pessoas foi retirada de uma população de 2.000 pessoas e 200 delas eram favoráveis a uma determinada proposta de instalação de um novo centro recreativo na localidade.
- Calcule um intervalo de 0,95 de confiança para a proporção, \(p\), de pessoas favoráveis à proposta.
- Qual deveria ser o tamanho de uma AAS para estimar \(p\) com confiança de 95% e um erro máximo aproximado de 3%?
Exercício 5.10 Numa população fictícia de \(N=6\) unidades, sabe-se que \(Y=\{0, 0, 1, 1, 1, 1 \}\). Suponha que se deseja estimar a proporção de “uns” na população por meio de uma AAS de tamanho \(n=4\).
- Encontre a distribuição amostral de \(\widehat p\), estimador da proporção de “uns”, e mostre numericamente que é um estimador não viciado para \(p\), a proporção populacional de “uns”.
- Sugira um estimador para a variância de \(\widehat p\) e verifique empiricamente se esse estimador é não viciado.